Sabemos que:
Si elevamos a la cuarta potencia tendremos:
En estos desarrollos se cumplen las siguientes leyes:
- Cada resultado tiene un término más que el exponente del binomio.
- El exponente de
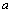en el primer término del desarrollo es igual al exponente del binomio, y en cada término posterior al primero disminuye en 1, hasta que desaparece (su exponente es cero). - El exponente de
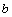en el segundo término del desarrollo es 1, y en cada término posterior a éste, aumenta 1, hasta llegar a ser igual que el exponente del binomio.
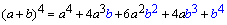
- El coeficiente del primer término del desarrollo es 1 y el coeficiente del segundo término es igual al exponente de
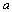en el primer término del desarrollo. - El coeficiente de cualquier término se obtiene multiplicando el coeficiente del término anterior por el exponente de
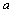en dicho término y dividiendo este producto entre el exponente de 
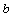en ese mismo término aumentado en 1.
Ejemplo: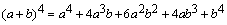
el coeficiente del tercer término se encuentra de la siguiente manera:
- El coeficiente del segundo término: 4
- El exponente de
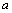del segundo término: 3 - El exponente de
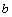del segundo término aumentado en 1 es: 1+1=2, entonces el coeficiente del tercer término es: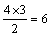
- El último término del desarrollo es
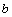elevado al exponente del binomio.
Los resultados anteriores constituyen la ley del binomio, que se cumple para cualquier exponente entero y positivo.
