Ejemplo 2
Resuelve el siguiente sistema de ecuaciones:
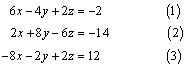
Solución
1. Seleccionamos una variable para ser eliminada y una ecuación que sirva de enlace con las otras dos.Eliminaremos la variable 
y la ecuación de enlace será la ecuación (3).
Eliminamos la variable elegida y obtenemos dos nuevas ecuaciones utilizando la ecuación de enlace y cada una de las otras opciones; se sigue el procedimiento utilizado en el sistema de 2 por 2.
- Eliminamos
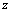de las ecuaciones (1 y 3), para ello multiplicamos la ecuación (1) por –1 y sumamos la ecuación resultante con la ecuación de enlace (Ecuación (3))
realizando la suma, tenemos que: 
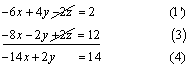
- Ahora, eliminamos
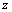de la ecuación de enlace y la ecuación (2), para ello multiplicamos la ecuación (3) por 3 y sumamos esta nueva ecuación a la ecuación (2) para obtener la ecuación (5).
realizando la suma, tenemos que:
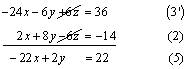
2. Las ecuaciones (4) y (5) forman un sistema de dos ecuaciones con dos incógnitas y se resuelven como lo vimos en el tema anterior.
- Eliminamos la variable
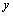multiplicando la ecuación (4) por –1 y la sumamos a la ecuación 5.
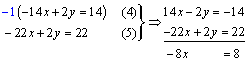por lo tanto 
- Sustituyendo el valor de
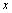en la ecuación (4) obtenemos el valor de 
.
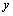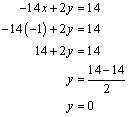
3. Se sustituyen los dos valores encontrados en cualquiera de las ecuaciones originales para encontrar la restante.
- Sustituimos el valor 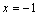de
y de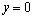 
en la ecuación (1) para encontrar el valor de 
:
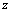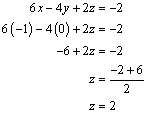
Por lo tanto, los valores que resuelven la ecuación son:
