Dominio, rango e imagen .

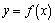
Los elementos de una función son:

• La variable x denominada variable independiente y la variable y denominada variable dependiente, ya que su valor depende del valor de x.

• El conjunto D de valores de x para los cuales tiene sentido calcular f(x) es llamado dominio.

• El conjunto F es llamado codominio.

• y = f(x) es llamada imagen de x bajo f y x es llamada preimagen de y.

• Al conjunto formado por todas las imágenes f(x) de las x del dominio, se le llama rango de la función y es subconjunto de .

Para especificar completamente una función, es necesario dar su dominio, así como su regla de asociación.

Para encontrar el dominio se debe considerar el conjunto de valores de x para los cuales tiene sentido calcular f(x).

 

Ejemplo 1                    Ejemplo 2

 

Existen diferentes tipos de funciones:

Función constante. A todas variables  del dominio se le asigna el mismo valor  en el codominio.


Función lineal. Es la función cuya regla tiene la forma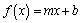

 

Función cuadrática. Es la función cuya regla tiene la forma

 

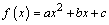
Función radical de índice par con subradical de la forma . Es la función de la forma

 

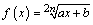
Función trigonométrica. Algunos ejemplos son , , etcétera.

 

Ejemplo 3      Ejemplo 4      Ejemplo 5       Ejemplo 6      Ejemplo 7

Ejercicio 1      Ejercicio 2       Ejercicio 3        Ejercicio 4