Con este objeto de aprendizaje se pretende que determine la representación gráfica de la parábola mediante sus elementos, que obtenga los elementos de la parábola mediante su gráfica, determine la ecuación ordinaria de ésta mediante sus elementos, obtenga los elementos de la parábola mediante su ecuación ordinaria, además de que plantee la expresión cuadrática a partir de un problema; que represente las relaciones entre las variables y obtenga la solución a un problema mediante la expresión cuadrática de una parábola o su gráfica.


Par�bola.

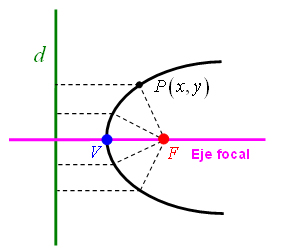
La parábola es el conjunto de puntos 16 que se encuentra a la misma distancia de un punto fijo 17, llamado foco, y de una recta fija 18, llamada directriz. El punto medio de la distancia del foco a la directriz se llama vértice 19.

20

La ecuación de la parábola es:

Con v�rtice en el origen y eje de simetr�a sobre el eje x

 

21

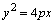
Y sus elementos son:

Elementos

Coordenadas del vértice

23

Coordenadas del foco

25

Ecuación del eje focal

EF:26

Ecuación de la directriz

D:27

 

  • Si 29 es positivo, la parábola abre hacia la derecha.

  • Si 30 es negativo, la parábola abre hacia la izquierda.

Con v�rtice en el origen y eje de simetr�a sobre el eje y


43

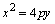
Y sus elementos son:

Coordenadas del vértice
24

Coordenadas del foco

44

Ecuación del eje focal

EF: 45

Ecuación de la directriz

D:46

 

  • Si 31 es positivo, la parábola abre hacia arriba.

  • Si 32 es negativo, la parábola abre hacia abajo.

Con v�rtice fuera del origen y eje de simetr�a paralelo al eje x

 

47

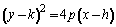
Y sus elementos son:

Coordenadas del vértice

49

Coordenadas del foco

51

Ecuación del eje focal

EF: 52

Ecuación de la directriz

D:53

 

  • Si 33 es positivo, la parábola abre hacia la derecha.

  • Si 34 es negativo, la parábola abre hacia la izquierda.

Con vértice fuera del origen y eje de simetría paralelo al eje y

 

54

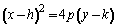
Y sus elementos son:

Coordenadas del vértice

50

Coordenadas del foco

55

Ecuación del eje focal

E.F.: 56

Ecuación de la directriz

D:57

 

  • Si 35 es positivo, la parábola abre hacia arriba.

  • Si 36 es negativo, la parábola abre hacia abajo.

Una ecuación de segundo grado en las variables x y y que carezca del término xy puede escribirse de la forma:

58

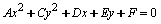
Si 59, 60 y 61, la ecuación representa una parábola cuyo eje es paralelo a (o coincide con) el eje x.

Si 62, 63 y 64, la ecuación representa una parábola cuyo eje es paralelo a (o coincide con) el eje y.

Ejemplo 1      Ejemplo 2      Ejemplo 3       Ejemplo 4

Ejercicio 1      Ejercicio 2

Ejercicio de aplicación