Ejemplo 1
Determina la gráfica de la parábola y su ecuación ordinaria, si ésta tiene vértice en el origen, 
y eje focal sobre el eje x.
Solución
La ecuación ordinaria de la parábola con vértice en el origen y eje focal sobre el eje x es 
, entonces sustituimos en ésta el valor 
y obtenemos la ecuación:
Entonces, la ecuación ordinaria de esta parábola es 
.
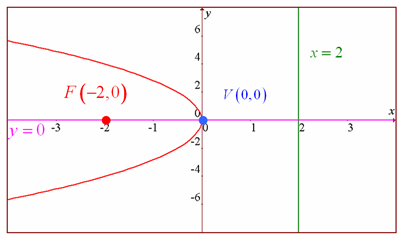
Para graficarla, sabemos que el eje focal está sobre el eje x (
) y que como 
es negativo, entonces abre hacia la izquierda. Identificamos en el plano cartesiano el punto 
que corresponde al vértice de la parábola, el punto 
que es el foco y enseguida trazamos la directriz cuya ecuación es 
, que para este caso es 
. Entonces, la gráfica es la siguiente:
