Con este objeto de aprendizaje se pretende que determine la representación gráfica de la elipse mediante sus elementos, que obtenga los elementos de la elipse mediante su gráfica, determine la ecuación ordinaria de la elipse mediante sus elementos, obtenga los elementos de la elipse mediante su ecuación ordinaria, además de que plantee la expresión cuadrática a partir de un problema; que represente las relaciones entre las variables y obtenga la solución a un problema mediante la expresión cuadrática de una elipse o su gráfica.
Elipse.
La elipse es el lugar geométrico de los puntos, tales que la suma de sus distancias a dos puntos fijos, llamados focos, es una constante positiva.
Los elementos de la elipse son los siguientes:
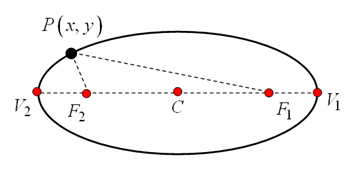
y
, representan los focos de la elipse.
La recta que pasa por los focos o eje focal.
Los puntos donde la curva interseca al eje focal, llamados vértices
y
de la elipse.
El segmento de la recta cuyos extremos son los vértices de la elipse es el eje mayor.
El punto medio del eje mayor, es el centro de la elipse.
El segmento perpendicular al eje mayor que pasa por el centro e interseca a la elipse en los puntos
y
, se llama eje menor. Por lo tanto,
y
son entonces los extremos dicho eje.
Cada uno de los segmentos del eje mayor, cuyos extremos son el centro de la elipse y los vértices (mitad del eje mayor), son el semieje mayor.
Cada segmento del eje menor, cuyos extremos son el centro de la elipse y los extremos del eje menor (mitad del eje menor), constituyen el semieje menor.
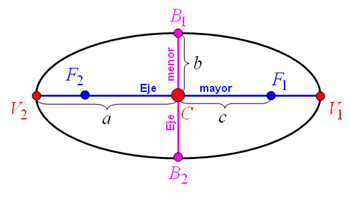
Podemos notar en la gráfica que siempre
.
La manera de medir el alargamiento de una elipse es por medio de su excentricidad, la cual se define como el cociente de la distancia focal entre el eje mayor.
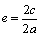
Observa que como
, entonces
. De esta forma, cuanto más cerca esté la excentricidad a cero, la elipse se parecerá más a un círculo, y mientras más cerca esté de uno, más alargada será.
La ecuación de la elipse es:
Con centro en el origen y eje focal sobre el eje x
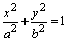
Sus elementos son:
Coordenadas del centro
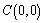
Distancia del centro de la elipse a cada foco
Coordenadas de los focos
y
Coordenadas de los vértices
y
Coordenadas de los extremos del eje menor
y
Longitud del eje mayor
Longitud del eje menor
Excentricidad
Con centro en el origen y eje focal sobre el eje y
Sus elementos son:
Coordenadas del centro
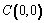
Distancia del centro de la elipse a cada foco
Coordenadas de los focos
y
Coordenadas de los vértices
y
Coordenadas de los extremos del eje menor
y
Longitud del eje mayor
Longitud del eje menor
Excentricidad
Con centro fuera del origen y eje focal paralelo al eje x
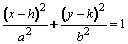
Sus elementos son:
Coordenadas del centro
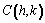
Distancia del centro de la elipse a cada foco
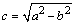
Coordenadas de los focos
y
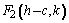
Coordenadas de los vértices
y
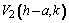
Coordenadas de los extremos del eje menor
y
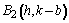
Longitud del eje mayor
Longitud del eje menor
Excentricidad
Con centro fuera del origen y eje focal paralelo al eje y
Sus elementos son:
Coordenadas del centro
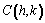
Distancia del centro de la elipse a cada foco
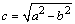
Coordenadas de los focos
y
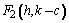
Coordenadas de los vértices
y
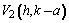
Coordenadas de los extremos del eje menor
y
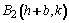
Longitud del eje mayor
Longitud del eje menor
Excentricidad
La ecuación de la elipse también puede escribirse en su forma general de la siguiente manera:
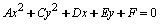
En donde
,
,
,
y
.
Los coeficientes
y
deben ser del mismo signo.
Ejemplo 1 Ejemplo 2 Ejemplo 3 Ejemplo 4 Ejemplo 5
Ejercicio 1 Ejercicio 2 Ejercicio 3 Ejercicio 4 Ejercicio 5
Ejercicio de aplicación