Ejemplo 4
Obtén la ecuación de la elipse que tiene su centro en el origen y cuyos focos son los puntos ![]() y
y ![]() , y uno de los vértices es
, y uno de los vértices es ![]() .
.
Solución
Podemos notar que el centro de la elipse es el origen y además el eje focal está sobre el eje y, ya que las abscisas de cada uno de los puntos dados son las mismas.
La ecuación de la elipse horizontal con centro en el origen y eje focal sobre el eje y es ![]() . Busquemos los datos que no conocemos.
. Busquemos los datos que no conocemos.
Como ![]() , entonces
, entonces ![]() . Sabemos que uno de los vértices es
. Sabemos que uno de los vértices es ![]() , entonces
, entonces ![]() .
.
El único dato que nos falta es ![]() , para calcularlo utilizamos la expresión
, para calcularlo utilizamos la expresión ![]() , ya que tenemos los valores de
, ya que tenemos los valores de ![]() y
y ![]() .
.
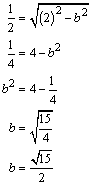
Para determinar la ecuación sustituimos los valores ![]() y
y ![]() en
en ![]() , entonces:
, entonces:
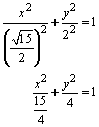
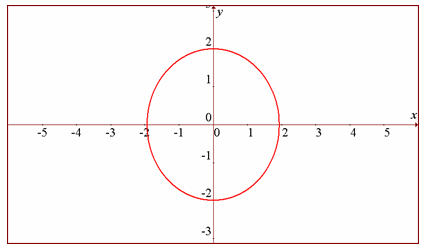
Su representación gráfica es la siguiente: