Con este objeto de aprendizaje se pretende que obtenga los valores y las expresiones que representan un lado de un triangulo rectángulo mediante el Teorema de Pitágoras y las funciones trigonométricas asociadas, así como los valores y las expresiones que representan el seno, el coseno y la tangente de uno de los ángulos de un triángulo rectángulo.
Teorema de Pitágoras y las funciones trigonométricas.
Cuando uno de los ángulos de un triángulo mide 90° se dice que se trata de un triángulo rectángulo. Al ángulo que mide 90° se le llama ángulo recto del triángulo.
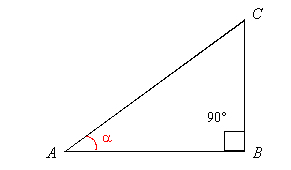
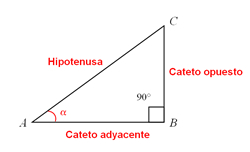
En la figura anterior, tenemos un triángulo rectángulo con vértices en los puntos A, B y C; además se ha indicado con a uno de sus ángulos no rectos.
Cada uno de los lados de un triángulo rectángulo recibe un nombre especial que depende del ángulo no recto que consideremos. En el caso de la figura anterior tenemos lo siguiente:
El segmento que va del punto Aal punto B
Cateto adyacente al ángulo
.
El segmento que va del punto B al punto C
Cateto opuesto al ángulo
.
El segmento que va del punto C al punto A
Hipotenusa del triángulo.
En general, no se menciona al ángulo a con lo cual tenemos que los lados de un triángulo rectángulo son: cateto opuesto, cateto adyacente e hipotenusa.
Una de las propiedades más interesantes de los triángulos rectángulos es conocida como el Teorema de Pitágoras, el cual relaciona el tamaño de cada uno de los lados del triángulo de la siguiente manera:
|
|
El cual también se escribe como:
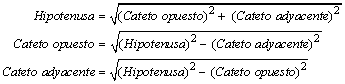
Una segunda propiedad de los triángulos rectángulos relaciona las medidas de sus lados con las funciones trigonométricas aplicadas a uno de sus ángulos no rectos.
Usando la notación de la figura anterior tenemos las siguientes identidades trigonométricas:
Función trigonométrica
Identidad trigonométrica
Seno
Coseno
Tangente
Cotangente
Secante
Cosecante