Con este objeto de aprendizaje se pretende que identifique la regla de asociación, dominio, rango y gráfica de las funciones logarítmicas.
Función logarítmica.
La función logarítmica es una función cuya regla de asociación tiene la forma
, donde
es un número en
llamado base.
- Su dominio son todos lon números reales positivos
cuando tenemos que
y cuando
el dominio son todos los reales negativos.
- Su rango son todos los números reales
.
La función logarítmica no está definida para los números negativos y el cero.
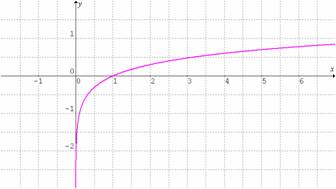
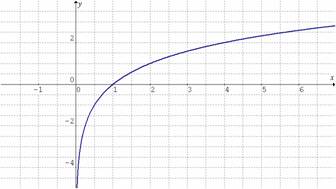
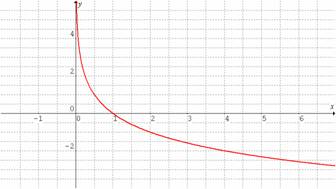
Observemos las gráficas de las siguientes funciones logarítmicas:
. Su dominio son todos los reales positivos, es creciente.
. Su dominio son todos los reales positivos, es decreciente.
Entonces, de acuerdo con las gráficas:
- Si
, la función
es decreciente.
- Si
, la función
es creciente.
La función logarítmica interseca al eje
en el punto
, es decir
; en general no interseca al eje
ya que es asintótica.
Ejemplo 1
Propiedades de las funciones logarítmicas
Entre todas las funciones logarítmicas existen dos especiales:
- Las que tienen base 10
, llamadas simplemente logaritmo.
- Las que tienen como base al número
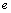
, llamadas logaritmo natural.
Para cambiar de base
a la base
de un logaritmo se utiliza la siguiente expresión:
- Si
se tiene
- Si
se tiene
Estas expresiones se utilizan para evaluar logaritmos.
Entre las funciones exponenciales y logarítmicas existe una relación muy estrecha, en general tenemos que si:
, entonces
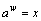
En especial se tiene que:
y
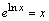
De aquí se desprenden las siguientes propiedades de los logaritmos: