Identifica la gráfica de la función 
, proporciona su dominio y su rango.
a)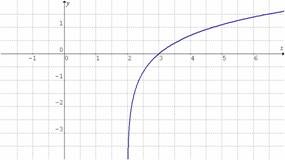
b)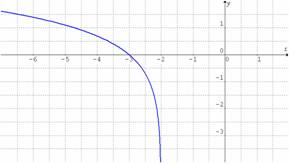 
c)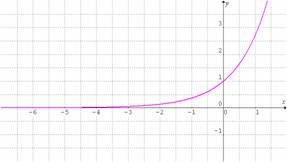 
Solución
Sabemos que el logaritmo natural es una función logarítmica que tiene como base al número 
, por lo tanto la gráfica es creciente, el dominio son los números tales que 
, es decir todos los números reales mayores que dos 
por lo que descartamos la gráfica b); observamos que la gráfica c) corta el eje 
lo cual no es posible para funciones logarítmicas; entonces la gráfica de la función 
es la gráfica a).