Esfuerzo y deformación

Carga multiaxial

 

Ya que hemos considerado, a través de la relación de Poisson, la deformación lateral dada una deformación normal, ahora debemos considerar el caso más realista donde el elemento mecánico está sometido a esfuerzos a lo largo de sus tres ejes de simetría, esto es, bajo carga multiaxial.

La herramienta principal para lograr el cálculo de la deformación que sufrirá en cada uno de los ejes, es el principio de superposición, que nos permite calcular cada deformación mediante la aportación que cada carga axial realiza en el eje considerado.

Teniendo en mente que al deformar en sentido positivo un eje cualquiera, con relación de Poisson positiva, establecimos que las deformaciones laterales tienen el signo negativo; podemos afirmar que la deformación unitaria total sufrida en un eje dado es la deformación normal más las dos aportaciones para las cuales el eje considerado es lateral. Si escribimos esta afirmación en función de los tres esfuerzos normales del elemento tenemos:

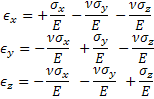
Estas relaciones son conocidas como la ley de Hooke generalizada para carga multiaxial.