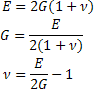En este objeto de aprendizaje se introducirá la deformación tangencial o cortante que forma parte de un esquema más generalizado de la ley de Hooke.
Esfuerzo y deformación
Deformación tangencial

Una vez que hemos considerado un estado general de esfuerzos multiaxiales, notemos que sólo hemos tomado en cuenta esfuerzos normales actuando en el elemento mecánico. Debemos recordar de la unidad anterior, que también existen los esfuerzos tangenciales o cortantes. Esta sección agregará estos esfuerzos con lo que lograremos un esquema más completo, es decir, un estado general de fuerzas.
Al aplicar una fuerza cortante, sobre las caras del elemento, éste reaccionará con una deformación caracterizada por una inclinación en las caras transversales a la dirección del esfuerzo cortante, deformación medible en forma de ángulo (en radianes). En la siguiente figura, ilustraremos este esquema para la cara superior de un paralelepípedo y también para dos esfuerzos cortantes en dos caras contiguas.
Como podemos observar en la figura de la izquierda, al aplicar un esfuerzo cortante en la cara xz, el efecto es que se modifica el ángulo entre esta cara y la cara zy, deformación que puede medirse con el ángulo interno mostrado. En la figura de la derecha se aplica un segundo esfuerzo cortante que por simetría, tiene el mismo valor, por lo que es natural observar que modifica al mismo ángulo que el de la cara superior.
Si el esfuerzo cortante no sobrepasa el límite de corte, la deformación obedecerá a la ley de Hooke, bajo las relaciones:
Donde la constante G es llamada módulo de rigidez o módulo cortante del material. Estas relaciones, junto a las ecuaciones establecidas en la ley de Hooke generalizada, representan una formulación aún más generalizada de esta ley. Nótese que sólo se definieron tres relaciones, pues las tres restantes, por simetría, son las mismas.
Relación E, G y ν
Una vez que se encuentra definido el módulo de Young E, el módulo de rigidez G y la relación de Poisson ν; a través de un análisis matemático se define la relación de estas variables como:
Lo que permite el cálculo de cualquiera de ellas conociendo las otras dos, para lo que será útil tener los despejes: