Como pudiste constatar, la deformación en un elemento circular dependerá de la distancia medida desde el eje de giro. Es decir, se habla de una distribución lineal de la deformación. Si nos referimos a un material que está sometido a esfuerzos por debajo de su límite de elasticidad, entonces sabemos que la deformación y el esfuerzo estarán relacionados por la ley de Hooke.

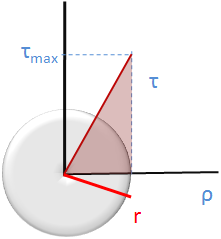
Sabemos, por lo aprendido en la unidad anterior, que el esfuerzo cortante y la deformación cortante están relacionados por:

Donde G ha sido definido como el módulo de rigidez. Con base en la ecuación determinada para la distribución de deformaciones, tenemos:

Por lo que al definir el esfuerzo cortante máximo como:

Obtenemos:

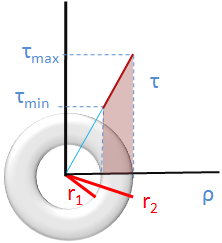
Es claro que, en el caso del esfuerzo cortante en el propio eje de giro, el esfuerzo mínimo es cero, pero en el caso de una sección transversal anular (un elemento circular hueco, como en la figura de arriba), la distribución de esfuerzos estará dominada por el esfuerzo mínimo y máximo que están relacionados linealmente por sus radios:

Donde r1 es el radio interior y r2 es el radio exterior.

Torsión elástica

A partir de lo anterior, en la mecánica de materiales se definen dos relaciones conocidas como fórmulas de torsión elástica:

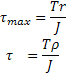
Donde J representa el momento polar de inercia de la sección transversal con respecto a su centro. En el caso de una sección circular tenemos:

Y para una sección anular se tiene: