Torsión

Ángulo de torsión en rango elástico

Cuando el estado de torsión al que es sometido el elemento mecánico no sobrepasa su límite de fluencia, sabemos que se encuentra en su región elástica, por lo que su deformación cumplirá con la ley de Hooke. Es muy importante encontrar, además de los esfuerzos y la deformación, el ángulo de torsión de un elemento sometido a un par de torsión. A partir de las ecuaciones que se han planteado, se podrá describir este ángulo en función del módulo de rigidez del material y su longitud.

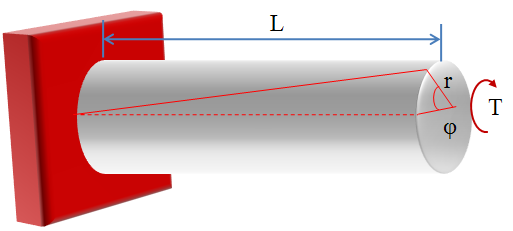
De la ecuación de deformación cortante unitaria máxima, podemos despejar el ángulo de torsión como:

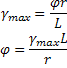
Por otro lado, la deformación cortante unitaria máxima puede despejarse como:

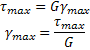
Pero la definición de esfuerzo cortante máximo se puede escribir también como:

Por lo que tenemos otra forma de describir la deformación cortante unitaria máxima:

Que al sustituirla en la ecuación del ángulo, forma una expresión para el cálculo del ángulo de torsión en función del torque aplicado, la longitud del elemento, el momento polar de inercia y el módulo de rigidez

En caso de tratarse de un elemento formado por varios segmentos de características diferentes, tenemos la generalización:

 

Nótese que todas estas formulaciones son válidas sólo en la región elástica del material en cuestión.