En este objeto de aprendizaje se definen las principales consideraciones en un elemento simétrico sometido a flexión pura.
Flexión pura
Esfuerzos en flexión pura

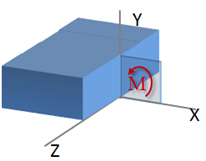
Volviendo a la figura del elemento sometida al par M y M' actuando en el plano de simetría del elemento, definiremos a dicho par como el momento flector de la sección trazada.

Este momento flector ya había sido relacionado con el esfuerzo flexionante al principio del curso, por lo que ahora trataremos detalladamente con este tipo de elementos, el esfuerzo y la deformación que se producen.
Es importante señalar que se asume que las secciones transversales del elemento, el cual es puesto en flexión, permanecen planas y que si cortamos una sección del elemento podremos encontrar que las fuerzas internas de la sección serán equivalentes al momento flector M.
Recordando que M es un par que consiste en dos fuerzas iguales y opuestas, sabemos que la suma de las componentes de estas fuerzas en cualquier dirección es cero y que el momento del par es el mismo alrededor de cualquier eje perpendicular al plano en donde actúan, y cero en cualquier eje que esté contenido en ese plano.
En consecuencia, podremos afirmar (asumiendo que el elemento se encuentra centrado descansando a lo largo el eje de coordenada X) que los momentos al rededor del eje Y son cero, mientras que los momentos en z son iguales a M, y las componentes del esfuerzo en el eje X suman cero; por ejemplo, para la sección mostrada en la figura.
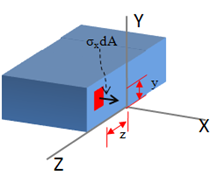
Podemos expresar estas condiciones del momento como:
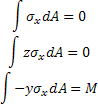
Lo que en la sección se expresa como: