Flexión pura

Deformación de un miembro simétrico

Para definir y calcular la deformación ocurrida en un elemento que se somete a flexión pura, trabajaremos con un elemento flexionado sometido a los pares M y M' que actúan en el plano de simetría del elemento. El elemento se flexionará de manera uniforme permaneciendo simétrico respecto al plano de simetría como lo muestra la figura siguiente:

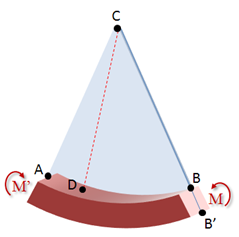
Observe que la línea de intersección AB, que antes de la flexión era recta, ahora forma un arco de centro C, note también que la línea longitudinal que une los puntos AB se ha acortado, mientras que la línea A'B' de la parte inferior del elemento se ha alargado. Dado que hemos asumido que las secciones transversales permanecen planas, sabemos entonces que sólo las componentes normales son no nulas.

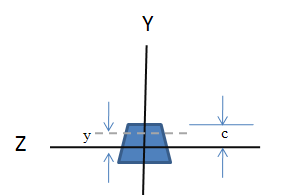
Como la sección superior del elemento se acorta, sabremos que los esfuerzos desarrollados en esa sección son esfuerzos de compresión, y como la sección inferior se alarga, habrá en ella esfuerzos de tensión. En consecuencia de esta distribución de esfuerzos de compresión y tensión, deberá existir una superficie dentro del elemento en el que el esfuerzo sea nulo; la línea longitudinal centrada que descansa sobre esta superficie es llamada el eje neutro y servirá para colocar el elemento en el eje de coordenadas, de manera tal que la distancia de cualquier punto a la superficie neutra se podrá determinar por la coordenada Y como lo observamos en la figura, donde además c representa el alto del prisma por arriba del eje neutro:

Con base en este eje neutro se investiga la deformación causada por la flexión pura, bajo el siguiente esquema de análisis:

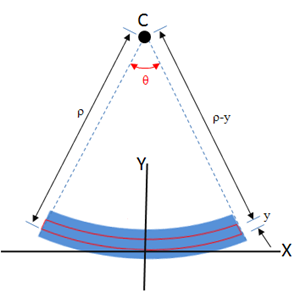
Donde podemos medir el radio (ρ) del arco sobre la que descansa el eje neutro del elemento deformado, además del ángulo θ que abarca con su longitud. Cuando el elemento no está deformado posee una longitud L que se puede calcular como el arco del eje neutro:

Por otro lado, se puede definir la longitud L' del arco ubicado a una distancia y del eje neutro que indica que existe un cambio en la longitud respecto al eje neutro.

Esta diferencia es la que se define como la deformación por flexión pura:

Resultado que permite definir la deformación unitaria longitudinal:

Con lo que se afirma que la deformación unitaria tiene variación lineal con respecto a la distancia de la superficie neutra. Si c es la distancia máxima a la superficie neutra, se puede definir el máximo valor absoluto de la deformación unitaria:

Y con ello la deformación unitaria tomará la forma: