Flexión pura

Esfuerzo y deformación en rango elástico

Cuando el sistema se encuentra a esfuerzos que están por debajo de su límite elástico, no habrá deformación permanente y la ley de Hooke será válida para calcular la deformación elástica. Si denotamos por E al módulo de elasticidad del elemento, al que consideraremos homogéneo, tendremos para el esfuerzo longitudinal:

Que se puede escribir como:

Donde σm representa el esfuerzo máximo:

Por otro lado, se puede probar que el eje neutro cruza por el centroide de la sección si los esfuerzos permanecen en el rango elástico. Tomando esta consideración y regresando a la ecuación del momento M:

Y sustituir el valor de el esfuerzo, tendremos:

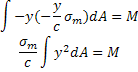
Donde la integral la identificamos como el momento de inercia (I), también llamado segundo momento, que al sustituir y despejar el valor del esfuerzo máximo nos da:

Por lo que para el esfuerzo normal tendremos:

Estas dos últimas ecuaciones son llamadas ecuaciones de flexión elástica. Por otro lado, como la razón I/c sólo depende de la geometría de la sección transversal, se le denomina módulo elástico de la sección y se representa por la letra S:

Con lo que definimos finalmente:

Observe que el esfuerzo máximo es inversamente proporcional al módulo eslástico de la sección, por lo que se busca utilizar un módulo S lo más grande posible.

Otro resultado importante, a partir de la deformación unitaria máxima:

Es la llamada curvatura de la superficie neutra, representada por el inverso del radio de curvatura y que se pude calcular como:

La cual podemos escribir en función del momento flector y el módulo eslástico como sigue:

Que es una formulación muy utilizada para determinar la curvatura con que se flexiona el elemento