Flexión pura

Deformaciones de una sección transversal

Aunque asumimos que las secciones transversales del elemento en flexión pura permanecen planas, esto no excluye que existan deformaciones dentro del mismo plano de la sección. Es decir, que podremos verificar deformación en las direcciones transversales y y z.

Estas deformaciones las podemos calcular por medio de la relación de Poisson propia de material con que es diseñado el elemento mecánico y cuya expresión matemática está dada por:

Que en función de la distancia respecto al eje neutro y es:

Lo que nos indica que se expande en ambas direcciones para elementos por encima del eje neutro; mientras que, por el contrario, los elementos por debajo del eje neutro se contraen. Es decir, que también existe un eje neutro transversal con forma de arco, con centro en C´ y radio ρ´=ρ/v.

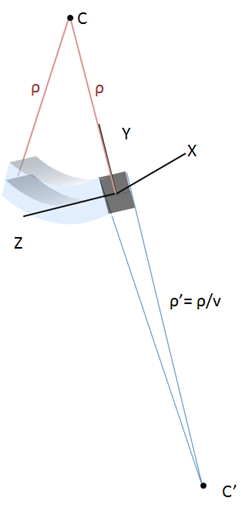
El inverso del radio de curvatura ρ' es la curvatura de la sección transversal y se denomina curvatura anticlástica, definida como: