Flexión pura

Carga axial excéntrica y flexión asimétrica

Carga axial excéntrica en un plano de simetría

Ahora se analizará un elemento que es sometido a una carga axial, cuya línea de acción no cruza por el centroide del elemento sometido al estado de fuerza.

Este tipo de análisis es muy útil en estructuras y elementos como prensas y arcos donde la línea de acción de la carga a la que son comúnmente expuestas, no corresponde con el centroide de la estructura y se quisiera analizar el estado de esfuerzos en que está sometida.

Suponga, por ejemplo, una pieza con forma de arco sometida a una carga axial con una línea de acción por debajo del centroide, como en la siguiente figura:

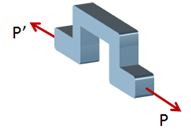
Note que el elemento posee un plano de simetría, y que en este plano es donde se aplica la carga. El centroide se ubica a una distancia d de la línea de aplicación de la carga, como apreciamos en el siguiente diagrama:

La forma equivalente de las fuerzas que actúan en este elemento se puede representar por la fuerza F aplicada en el centroide y a un par M que actúa en el plano de simetría del elemento.

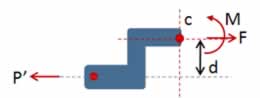
Si aplicamos las condiciones de equilibrio, se podrá notar que la fuerza F deberá ser igual y opuesta a P' mientras que el momento M será igual y opuesto al momento de P' con respecto a C, es decir:

En los análisis de este tipo, se puede también encontrar el esfuerzo desarrollado, como la suma de dos esfuerzos, uno céntrico y uno de flexión. Es decir, el correspondiente a la fuerza F y otro al momento M, los cuales podemos escribir de forma conveniente como:

Donde A es el área transversal e I el momento centroidal de inercia, y se mide con respecto al eje centroidal de la sección.

Flexión asimétrica

En ocasiones es necesario analizar elementos que se encuentran bajo un estado de flexión en un plano que no corresponde al de simetría del elemento. Si el elemento posee planos de simetría, es posible descomponer el momento flector como dos momentos que actúan en los planos de simetría del elemento y determinar el esfuerzo por superposición de los efectos de cada uno de los componentes del esfuerzo.

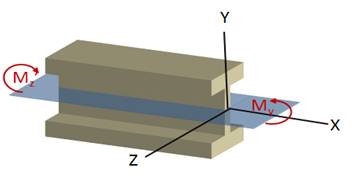
Tomemos como ejemplo el elemento de la figura que se encuentra sometido a un par de momentos flectores M y M´, actuando en un plano oblicuo formando un ángulo θ con el plano XY.

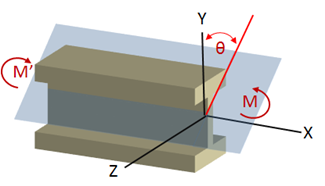
El momento flector se descompone en sus componentes Mz y My como:

Actuando en los planos XY y XZ respectivamente, como lo vemos en las siguientes figuras:

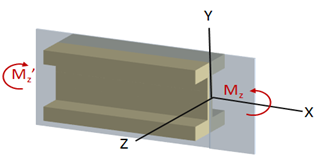
Para calcular el esfuerzo desarrollado en el elemento, se utiliza el principio de superposición, con lo que se define la ecuación: