Flexión pura

Ejercicios resueltos

Problema 4.1 (Mecánica de Materiales Ferdinand P. Beer et al., cuarta edición)

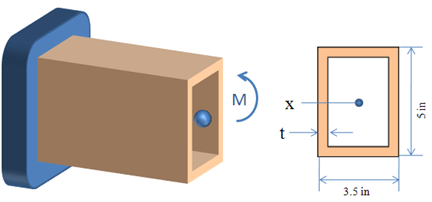
El tubo  rectangular que se presenta  en la figura se  obtiene de una aleación de aluminio con= 40 ksi, y = 60 ksi y E=10.6x106 psi. Calcule a) el momento flector   para el cual  el factor de seguridad será 3.00, b) el radio de curvatura correspondiente  del  tubo.

Solución

Momento de inercia. Considerando la sección transversal del tubo como la diferencia de los dos  rectángulos, como se muestra en la figura y recordando la fórmula del momento centroidal de inercia de un rectángulo, se  tiene:

Esfuerzo admisible. Con un factor de seguridad  de  3.00 y con un esfuerzo último de  60 ksi:

Puesto que , el tubo permanece en el rango elástico y pueden aplicarse los resultados que hemos analizado.

a) Momento flector. Si  entonces:

b) Radio de  curvatura. Como E=10.6x106 psi, se sustituye este valor y los obtenidos de    y    para encontrar:

Problema 4.2 (Mecánica de Materiales Ferdinand P. Beer et al., cuarta edición)

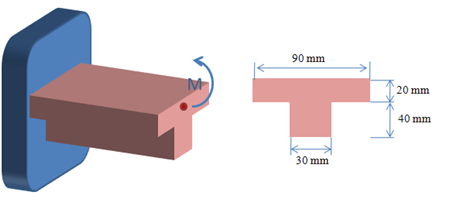
Una sección de una máquina de  hierro colado se somete a un par de , tal que como se muestra en la figura. Si  y se desprecia el efecto del filete, determine a) los esfuerzos máximos de tensión y compresión en el elemento fundido, b) su radio de curvatura.

Solución

Centroide. Se  divide la sección transversal en T en dos rectángulos y se escribe:

	Área, mm2
1	(20)(90) =1 800	50
2	(40)(30) =1 200	20

 

Momento centroidal de inercia. Se utiliza el teorema de los ejes paralelos para hallar el momento de inercia de cada rectángulo, con respecto al eje que pasa por el centroide de la sección compuesta. Sumando esos momentos de  inercia, se tiene:

a. Esfuerzo máximo de tensión. Como los momentos aplicados flexionan la fundición hacia abajo, el centro de curvatura se sitúa debajo de la sección. Su tensión máxima ocurre en el punto A, que es el más alejado del centro de curvatura:

Esfuerzo máximo de compresión. Se produce en el punto B; se tiene

b. Radio de curvatura. De la ecuación de radio de curvatura se tiene: