Carga transversal

Esfuerzos cortantes en miembros de pared delgada

Hemos visto cómo determinar el corte longitudinal  ejercido sobre las paredes de un elemento de viga de forma arbitraria y cómo determinar el flujo cortante  correspondiente. Estas ecuaciones se utilizarán en esta sección para calcular tanto el flujo cortante como el esfuerzo cortante promedio en elementos de pared delgada, por ejemplo, en patines de vigas de patín ancho y de  vigas  de caja o en las paredes de  tubos estructurales.

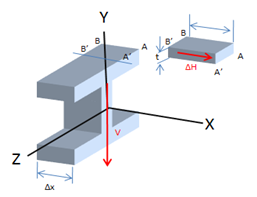
Considere, por ejemplo, un segmento con longitud  de una  viga de patín ancho y  sea  el corte vertical en la sección transversal mostrada. Se desprende un elemento   del patín superior. El corte longitudinal  ejercido sobre el elemento puede obtenerse de la ecuación:

Dividiendo  entre el área  del corte, se obtiene que para el esfuerzo cortante promedio ejercido sobre el elemento, la misma expresión que se obtuvo en la sección para el caso de un corte horizontal:

Debe notarse, sin embargo, que  representa ahora el valor promedio del esfuerzo cortante   ejercido sobre el corte vertical. Pero  como el espesor  de la aleta es pequeño hay  muy poca variación de   a través del corte. Así,  recordando que , se concluye que la componente horizontal  del esfuerzo cortante en cualquier punto de la sección  transversal de la aleta puede obtenerse mediante la ecuación del promedio, donde  es el primer  momento del área sombreada con respecto al eje neutro.

Hasta ahora se ha supuesto que todas las cargas actuaban en un plano de simetría  del elemento, en el caso de elementos con dos planos de simetría, como la viga de aleta de la figura o alguna viga-cajón, cualquier carga aplica a través del centroide de una  sección transversal puede descompensarse en componentes a lo largo de los ejes de simetría de la sección. Cada componente provocará  que el elemento  se flexione en un plano de simetría; los esfuerzos cortantes correspondientes se obtienen mediante la ecuación de . el principio  de la superposición puede usarse para hallar los esfuerzos resultantes.

Sin embargo, si el elemento considerado carece de un plano de simetría o si posee uno solo y se le somete a una carga no contenida en ese plano, se observa que el elemento se flexiona y tuerce al mismo tiempo, excepto cuando la carga se aplica en un punto específico llamado centro de cortante. Observe que el centro de cortante generalmente no coincide con el centroide de la sección transversal.