Transformaciones de esfuerzo-deformación

Transformación de esfuerzo plano

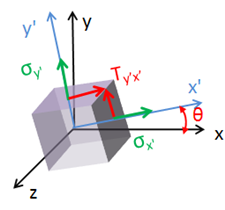
Para analizar la transformación de esfuerzo plano, se asume un estado de esfuerzo plano en un punto que por lo general se hace coincidir con el origen del espacio, con el eje z libre de esfuerzo, y que ha girado respecto al eje z un ángulo θ, quedando un elemento como el de la figura mostrada. Es de interés conocer cómo se ha modificado el estado de esfuerzos y encontrar una relación respecto al estado de esfuerzos normales y tangentes originales.

A través de la aplicación de la suma de momentos y utilizando identidades trigonométricas, se puede probar que las ecuaciones que definen la transformación de los esfuerzos están dadas por:

 

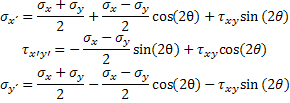
como consecuencia, si sumamos la expresión del esfuerzo normal en x' y en y', podemos verificar la relación:

 

de donde podemos afirmar que: la suma de los esfuerzos normales ejercida sobre un elemento cúbico de material, no depende en forma alguna de la orientación del elemento.