Transformaciones de esfuerzo-deformación

Esfuerzos principales, esfuerzos cortantes máximos

A partir de las ecuaciones descritas en el objeto de aprendizaje anterior, se estudiará la manera de definir los llamados esfuerzos principales, como los máximos esfuerzos normales y cortantes de un elemento sometido a esfuerzo plano. La idea subyacente es encontrar una expresión paramétrica de las ecuaciones en la forma de la ecuación de la circunferencia. Para este fin usamos la ecuación de esfuerzo normal en el eje x como:

al elevarse al cuadrado y haciendo esta operación en la ecuación del esfuerzo cortante, tendremos, respectivamente:

 

al sumar estas dos últimas ecuaciones, simplificando obtendremos:

 

a la que le daremos forma de ecuación de la circunferencia con los parámetros:

 

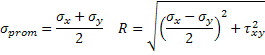
lo que finalmente se puede escribir como:

 

que representa la ecuación de la circunferencia centrada en (σprom, 0) y radio R, que podemos graficar como:

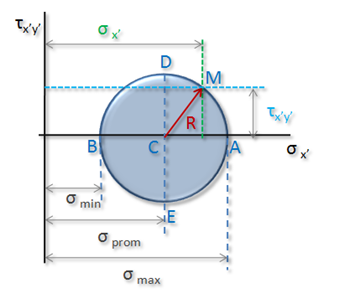
A partir de las ecuaciones desarrolladas podemos, por ejemplo, encontrar el ángulo θp, en el cual el esfuerzo cortante sea nulo, que en la gráfica ocurre en los puntos A y B:

 

de manera similar podemos investigar el ángulo θs en el cual el esfuerzo cortante es el máximo, que sabemos ocurre cuando el valor de esfuerzo normal se encuentra precisamente en el promedio (punto D), de donde podemos deducir la ecuación:

 

es claro que el valor máximo del esfuerzo normal, así como el mínimo, se pueden encontrar sumando o restando –respectivamente– el valor del radio R del centro, que está representado por σprom, con lo que tendremos:

 

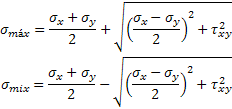
de manera equivalente podemos deducir que el valor máximo del esfuerzo cortante es precisamente el valor del radio, por lo que lo definimos como:

 

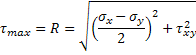
Estos tres últimos esfuerzos son los llamados esfuerzos principales. No se debe olvidar que esta formulación sólo es válida para rotaciones en el plano de esfuerzo, puesto que una rotación en el eje z podría someter al elemento a esfuerzos cortantes mayores.