En este objeto de aprendizaje se expondrá el concepto del círculo de Mohr para esfuerzo plano y su utilidad para calcular esfuerzos máximos en un elemento.
Transformaciones de esfuerzo-deformación
Círculo de Mohr para el esfuerzo plano
El círculo de Mohr es una técnica gráfica para análisis de esfuerzo plano basada en el trazo de una circunferencia como la que se realizó en la sección anterior. El círculo de Mohr simplifica muchos problemas donde es de interés encontrar los esfuerzos máximos, mínimos ya sea a partir de la posición original del estado de esfuerzos, o de un estado de esfuerzos que ha girado respecto al eje del esfuerzo plano.
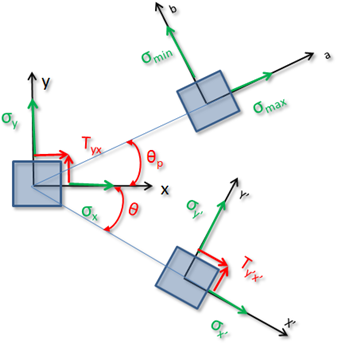
Para llevar a cabo el trazo del círculo de Mohr, se debe considerar un elemento cuadrado sometido a esfuerzo plano como en la figura siguiente:
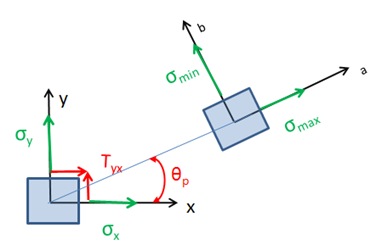
Se dibujan los puntos: X con coordenadas (σx, -τxy) y Y en (σy, τxy). Es natural que un punto quede en la región por encima de la recta del esfuerzo y otro por debajo de ésta. Se unen estos dos puntos mediante una línea recta que cortará a la recta de esfuerzo en un punto que será el centro del círculo de Mohr y la línea XY será el diámetro. Con este procedimiento, el centro del círculo se encontrará exactamente en (σprom, 0) y el radio R será tal y como se definió en la sección anterior, por lo que los puntos donde la circunferencia corta al eje de esfuerzo A y B serán, respectivamente, el esfuerzo mínimo σmin y máximo σmax.
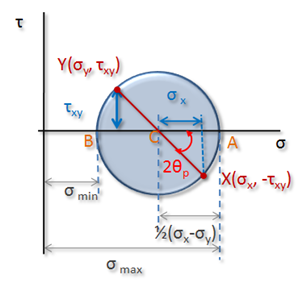
De la figura podemos deducir que el ángulo XCA es precisamente el ángulo 2θp, por lo que será muy fácil su cálculo. Es importante señalar que el círculo de Mohr está definido de manera única, por lo que este mismo procedimiento puede realizarse a partir de un estado de esfuerzos que ha sido girado respecto al eje del esfuerzo plano.