En este objeto de aprendizaje se introducen algunas fórmulas útiles para calcular el esfuerzo en recipientes de pared delgada, que están sometidos a un estado de esfuerzos dada la presión del contenido.
Transformaciones de esfuerzo-deformación
Esfuerzos en recipientes a presión de pared delgada
Otra consideración, en relación con los esfuerzos, es aquella relacionada a contenedores o tuberías, que por lo general contienen alguna sustancia a una presión mayor a la atmosférica. La presión ejerce una fuerza por sobre las paredes del recipiente o tubería y es de interés conocer el esfuerzo desempeñado por el elemento mecánico para saber que resistirá las condiciones de trabajo impuestas.
Contenedor cilíndrico
Considere un recipiente cilíndrico con radio interior r y con ancho de pared t. Existen dos esfuerzos normales actuantes sobre la pared del contenedor, uno es llamado esfuerzo tangencial y el segundo: esfuerzo longitudinal. En la figura se muestra un esquema de estos dos esfuerzos.
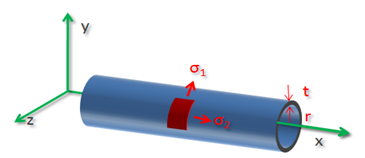
el análisis de los esfuerzos arroja que el esfuerzo tangencial (llamado también esfuerzo de costilla) para un recipiente de estas características esta dado por:
donde p es la presión del fluido, r el radio interior y t el ancho de la pared. Para este mismo caso, se tiene la expresión del esfuerzo longitudinal como:
finalmente, para este tipo de recipientes, se calcula el esfuerzo cortante máximo al que está sometida la pared, cuyo resultado es:
Contenedor esférico
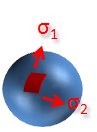
Otra clase de recipientes de pared delgada (muy utilizada) es la esférica, de la cual podemos presentar el cálculo del esfuerzo de costilla y longitudinal, que en este caso especial son iguales:
a su vez, el esfuerzo cortante máximo estará dado por: