A través de este recurso podrás reconocer de manera clara y sencilla, los métodos estadísticos utilizados para compensar y minimizar el efecto de los errores aleatorios.
Introducción a la instrumentación, medidas de presión, flujo, nivel y temperatura Análisis estadístico del error En análisis estadístico de errores aleatorios, la raíz cuadrática de las desviaciones o desviación estándar es una ayuda muy valiosa. El valor más probable de una variable medida es la medida aritmética de un número de lecturas tomadas. Se representa por la siguiente expresión.
|
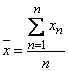
donde:
= media aritmética
= lecturas tomadas
= número de lecturas
La desviación estándar de un número finito de datos 
, es igual a la raíz cuadrada de la suma de todas las desviaciones cuadradas individuales, divididas entre el número de lecturas. En forma matemática:
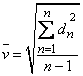
= valor medido
= media aritmética
= número de lecturas
Otra expresión usada con el mismo propósito es la varianza, la cual se expresa de la siguiente manera:
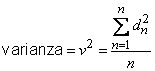
La ley normal del error o gaussiana constituye la base del estudio analítico de los efectos aleatorios. Las siguientes proposiciones cualitativas se basan en la ley de distribución normal:
-
Todas las observaciones incluyen pequeños efectos de distorsión, llamados errores aleatorios.
-
Los errores aleatorios pueden ser positivos o negativos.
-
Hay igual probabilidad de errores aleatorios positivos o negativos.
Las posibilidades, así como la forma de la curva, de distribución de error se pueden establecer de la siguiente manera:
-
Son más probables los pequeños errores que los grandes.
-
Los errores grandes son muy improbables.
-
Hay igual probabilidad de que ocurran errores positivos y negativos, de manera que la probabilidad de un error dado será alrededor del valor cero.
-
La curva de distribución del error se muestra en la siguiente figura:
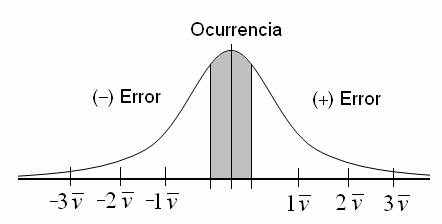
Para datos distribuidos normalmente y según la distribución de Gauss mostrada en la figura anterior, alrededor del 68% de todos los casos quedan entre los limites 
y 
de la medida.
Ejemplo
Diez mediciones de resistencia dan 101.2
, 101.7, 101.3, 101.0, 101.5, 101.3, 101.2, 101.4, 101.3 y 101.1. Si se considera que sólo presentan errores aleatorios, calcular:
a) La medición aritmética.
b) La desviación estándar de las lecturas.
c) El error probable.
Solución:
a)
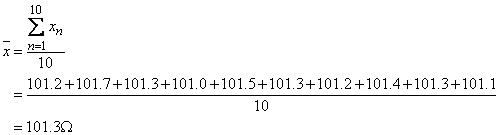
b)
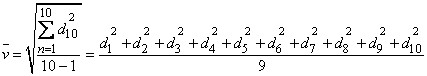
entonces:
de modo que:
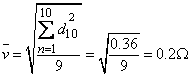
c) El error probable se calcula por:
De modo que en base a esto, el error probable se define como:
Este valor es probable en cuanto a que hay igual probabilidad de que alguna medición tenga un error aleatorio no mayor que 
.