Realizaci�n de la soluci�n
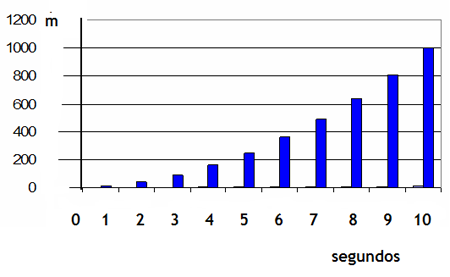
La gr�fica muestra la altura que en metros va alcanzando el cohete conforme pasa cada segundo. El eje vertical presenta los valores de h (t) en metros y el eje horizontal muestra los valores de t en segundos transcurridos desde el despegue.
a. Al acabarse el combustible, t = 60 segundos. Seg�n la relaci�n [10.6] la altura alcanzada es:
h (60s) = 10 (60)� m = 36000 m
h (60s) = 36000 m = 36 km � [10.7]
b. La velocidad media o promedio al agotarse el combustible es vm:
Vm = distancia recorrida/ tiempo de recorrido = 36000m/60s = 600m/s
Vm = 600m/s �. [10.8]
c. �Qu� valor presentar� cuanto hayan transcurrido 8 segundos?
No se trata de calcular la velocidad promedio al transcurrir 8 segundos, ese valor es h (8) m/ 8 s = 80 m/s. Lo que se pide es el valor que marcar�a un od�metro instalado en el cohete as� como ocurre en un autom�vil cuyo veloc�metro marca el valor de la rapidez del auto en todo el recorrido.
La gráfica [10.3] muestra que para intervalos iguales de 1 segundo se recorren distancias cada vez más grandes, es decir, el cohete va aumentando su velocidad.
Como fue establecido en la estrategia de solución, lo que sí se puede calcular es la velocidad en el intervalo de una décima de segundo antes del valor 8 segundos y también la velocidad en el intervalo de una décima después de ese tiempo y por la segunda hipótesis que se expuso, se esperaría que el valor buscado estuviera entre esos dos valores.
La velocidad V<8 en el intervalo t1 = 7.9s yt2 = 8s se obtiene como:
V<8 = {(h (t2) - h (t1)}/(t2 - t1) = 10(t2² - t1²)))/(t2 - t1) … [10.9]
V<8 = (15.9/0.1) m/s = 159 m/s … [10.10]
La velocidad v>8 en el intervalo t1 = 8 s y t2 = 8.1 s se obtiene como:
V>8 = {h (t2) - h (t1)}/(t2 - t1) = 10(t2² - t1²)/(t2 - t1) … [10.11]
V>8 = (16.1/0.1) m/s = 161 m/s … [10.12]
La velocidad que presenta el cohete cuando han transcurrido 8 segundos de viaje está entre dos valores:
V<8 < V8 < V>8 … [10.13]
159 m/s < V8 < 161 m/s … [10.14]
Si se consideran intervalos de tiempo más cercanos al valor de t = 8 segundos, se obtendría una mayor aproximación al valor de la velocidad que nos interesa conocer. Si se designan por V'<8 y V'>8 los nuevos valores a calcular con intervalos de tiempo de 0.01 s antes y después de t = 8 segundos se obtiene:
V'<8 = 10 m ((8) ² – (7.99) ²)/(0.01)s = 159.9 m/s … [10.15]
V'>8 = 10 m ((8.01) ² – (8) ²)/(0.01)s = 160.1 m/s … [10.16]
De manera que ahora se obtiene para V8:
159.9 m/s < V8 < 160.1 m/s … [10.17]
Una tercera aproximación para los extremos del intervalo donde se ubica el valor de V8, designados por V″<8 y V″>8 se obtiene:
159.99 m/s < V8 < 160.01 m/s … [10.18]
Con estos resultados tenemos una sucesión de valores de velocidad para tiempos anteriores a 8 segundos: 159, 159.9, 159.99,…, cuyo límite es 160 m/s
La sucesión de valores de velocidad para tiempos posteriores a 8 segundos es: 161, 160.1, 160.01,…, cuyo límite es 160 m/s
Puede afirmarse que dentro de un margen de error, que se reduce conforme se hacen mayores aproximaciones, el valor para la velocidad del cohete cuando han transcurrido ocho segundos desde su despegue es:
V8 = 160 m/s … [10.19]