Elementos básicos y variables de los circuitos eléctricos

Ejercicios resueltos

1.- Encuentra el valor de:
a) Resistencia medida en la entrada (R ent).
b) Resistencia medida en la salida (R sal).
c) Resistencia desde A hasta el nodo inferior.

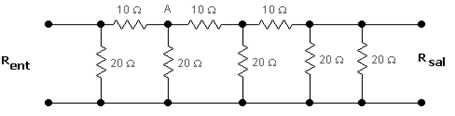
a) R(ent)

1) (20 || 20) +10 =20
2) (20 || 20) +10 =20*
3) (20 || 20) +10 =20
4) (20 || 20) = 10Ω

b) R(sal)

1) (20+10)||20= 12
2) (12+10)||20= 10.476
3) (10.476+10)||20= 10.118
4) 10.118||20= 6.719Ω

c) R(A)

(20+10)=30||20 (R inferior de A) || 20 (Reducción de R (ent) hasta donde aparece *) = 7.5Ω

2.- En la red mostrada encuentra:

a) Req, si R=40 Ohms,
b) R, si Req=26 Ohms,

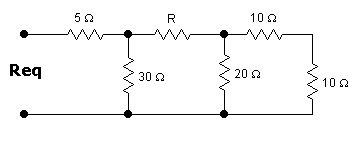
a)   Req

1) (10+10)||20=10
2) (10+40)||30=18.75
3) 18.75+5=23.75Ω

b)   R

1) (26-5)=21
2) (1/21 – 1/30)=1/R2
3) R2=70
4) R= 70 – [20|| (10+10)]=60Ω

3.- Encuentra el valor de la resistencia equivalente "vista" entre los puntos A-B. No hay ningún resistor en serie o en paralelo con otro.
R1 = 4 k Ohms
R2 = 3 k Ohms
R3 = 2 K Ohms

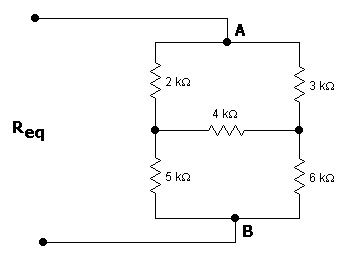
Este ejercicio lo podemos resolver mediante transformación delta-estrella, se puede convertir la parte superior o la inferior, aquí ejemplificamos con la superior para que quede de la siguiente manera:

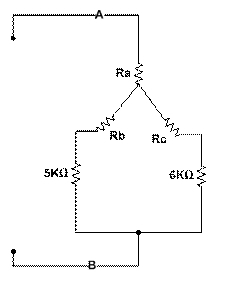
Nota que se utilizan las resistencias que estarían a los lados de la nueva a calcular, por ejemplo Ra la obtenemos de R3 y R2.

Ra = (R2 x R3) / (R1 + R2 + R3)
Rb = (R1 x R3) / (R1 + R2 + R3)
Rc = (R1 x R2) / (R1 + R2 + R3)

Ra = (3k x 2k) / (4k + 3k + 2k)=0.666K
Rb = (4k x 2k) / (4k + 3k + 2k)=0.888K
Rc = (4k x 3k) / (4k + 3k + 2k)=1.33K

Simplificando:

(5kΩ+0.888KΩ)||(6KΩ+1.333kΩ)=3.2657
3.2657KΩ +0.666KΩ =3.932KΩ