Técnicas de análisis de circuitos

Ejercicios resueltos

1.- Con base en LKV, ¿cuál es el voltaje Vo?

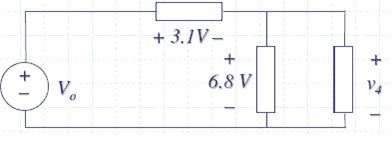
Vo – 3.1 – 6.8 = 0
Vo= 3.1 + 6.8
Vo= 9.9 V

2.- Con base en LKC, encuentra los valores de todas las corrientes.

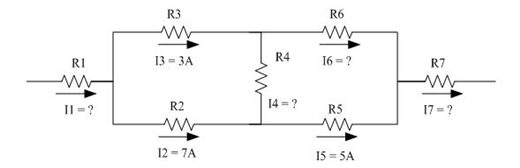
I1 = I2 + I3 = 7 + 3 = 10A

I2 = I4 + I5
I4 = I2 - I5 = 7 - 5 = 2A

I6 = I3 + I4 = 3 + 2 = 5A

I7 = I6 + I5 = 5 + 5 = 10A

3.- Mediante el método de mallas encuentra las corrientes correspondientes en cada malla.

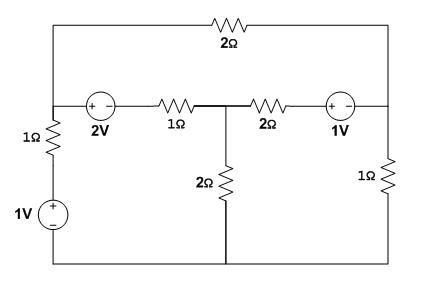
Supongamos todas las corrientes en el sentido de las manecillas del reloj.
Malla 1:     I1 (1+1+2) – I2 (2) – I3 (1) = 1-2
Malla 2:   - I1 (2) + I2 (2+2+1) – I3 (2)= -1
Malla 3:   - I1 (1) – I2 (2) + I3(2+2+1)=2+1

Malla 1:     4 I1– 2 I2 – I3 = - 1
Malla 2:   - 2 I1 + 5 I2  – 2 I3 = -1
Malla 3:   - I1 – 2 I2 + 5 I3 = 3

Podemos resolver el sistema de ecuaciones por matrices, por suma y resta, por sustitución, etcétera.
I1= 117 mA
I2= 20 mA
I3= 631mA

Practica con otros valores

4. Encuentra la corriente que pasa por la resistencia de 20KΩ utilizando el principio de superposición.

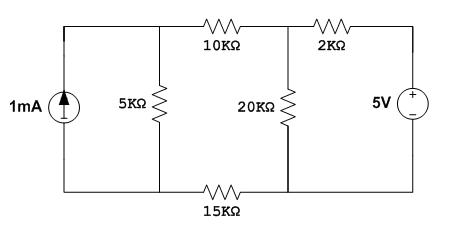
Para la fuente de 1mA
Se cortocircuita la fuente de 5V

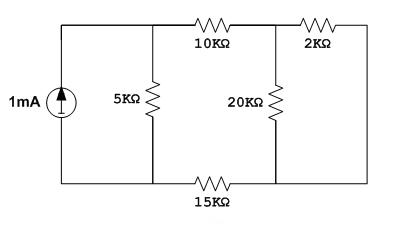
Hacemos el paralelo de 2K y 20K = 1.81K
La corriente de 1 mA se divide entre la resistencia de 5K y la serie de 10K, 1.81K y 15K, por lo que aplicamos divisor de corriente.
I= 1mA[5K /(5K+10K+1.81K+15K)] = 0.16 mA
Esa corriente se divide nuevamente entre la resistencia de 20K y la de 2K
I = 0.16 [2K/(20K+2K)]=0.014mA

Para la fuente de 5V

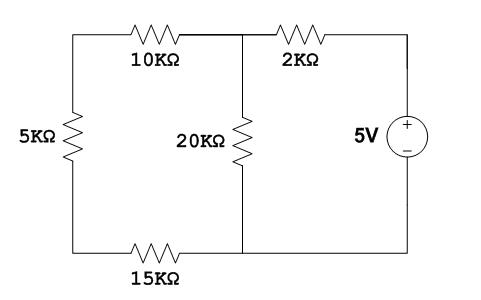
Se abre la fuente de 1mA
Simplificamos dejando sólo dos resistencias en serie
(5K + 10K + 15K)|| 20 K = 12K
V12K= 5 [12/(12+2)]= 4.28 V
Por Ley de Ohm
I=4.28 / 20K = 0.214 mA
Sumando el efecto de ambas fuentes
0.014mA + 0.214mA = 0.228mA