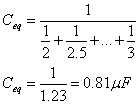Elementos de almacenamiento de energía eléctrica

Ejercicios

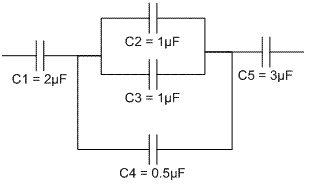
1. Obtener la capacitancia equivalente del siguiente arreglo:

Podemos observar que C2, C3 y C4  se encuentran en paralelo, por lo tanto, los sumamos directamente:
Ca= 1μF+1μF+0.5μF=2.5μF
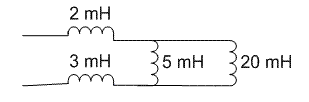
Ahora tenemos C1, Ca y C5 en serie:

2. Calcule la inductancia equivalente del circuito siguiente.

Realizamos el paralelo de 5mH y de 20mH

(5mH || 20mH) = 1/(1/5+ 1/20) = 4mH
Ahora la serie de todos los elementos
Leq= 2mH + 3mH + 4mH = 9mH

3. El interruptor en el circuito ha estado en la posición x por un largo tiempo.  En t=0, el interruptor se mueve hasta la posición y.  Determine:
a) vc (t) para t ≥ 0
b) vo (t) para t ≥ 0+
c) io (t) para t ≥ 0+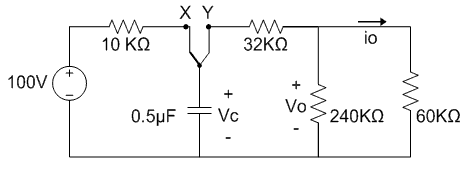

a) Debido a que el interruptor ha estado en la posición x durante mucho tiempo, el capacitor de 0.5μF se cargará hasta 100 V y será positivo en la terminal superior.  Es posible reemplazar la red resistiva conectada al capacitor en t = 0+ con una resistencia equivalente de 80KΩ.  La constante de tiempo es RC = (0.5 x 10-6) (80 x 103)= 40ms.  Consideramos t=1.
Vc(t) = 100 e ^-25t , t ≥ 0

b) La manera más fácil de encontrar vo(t) es notar que el circuito resistivo forma un divisor de voltaje entre las terminales del capacitor, por lo que realizamos el divisor entre la resistencia de 32K y la de 48K que se formó de (60K || 240K).
Vo(t)= 48/80 Vc (t) =60 e ^-25t V, t ≥ 0+

c) Se encuentra la corriente io(t) a partir de la ley de Ohm.
io(t) = vo (t)/ (60x103) = e ^-25t mA, t ≥ 0+

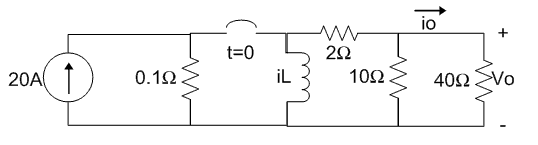
4. El interruptor de la siguiente figura ha permanecido cerrado por un largo tiempo antes de abrirlo en t=0.  Determine:
a) iL (t) para t ≥ 0
b) io (t) para t ≥ 0+
c) vo (t) para t ≥ 0+

a) El interruptor ha estado cerrado largo tiempo, por lo que se sabe que el voltaje en el inductor debe ser cero en t=0-. En consecuencia, la corriente inicial en el inductor es 20 A y t=0-.  Por lo tanto, iL (0+) también es 20 A, debido a que en un inductor no puede ocurrir un cambio instantáneo en la corriente reemplazando el circuito resistivo conectado a la terminal del inductor con un solo resistor:
Req = 2 + (40 || 10) = 10Ω
La constante de tiempo del circuito es L/Req, o 0.2s, obteniéndose la expresión para la corriente del inductor como
iL (t)= 20e^-5t A , t ≥ 0
b) Se determina la corriente en el resistor de 40Ω de modo más sencillo utilizando la división de corriente, esto es:
io=- iL [10/(10+40)]
io(t) = -4e^-5t A, t ≥ 0+
c) Se encuentra el voltaje Vo mediante la aplicación directa de la ley de Ohm.
vo(t) = 40io = -160e^-5t V, t ≥ 0+