Con este recurso en particular se pretende dar un repaso a los números complejos, ya que serán necesarios para el análisis de circuitos en ca.
An�lisis senoidal en estado estable
Repaso de números complejos
Los números complejos permiten la extracción de raíces cuadradas de números negativos. La capacidad para manipularlos es de gran utilidad en el análisis de circuitos, ya que simplifican la solución de problemas.
Notación
Existen dos maneras de designar a un número complejo: la forma cartesiana o rectangular; y la forma polar o trigonométrica.
Forma rectangular
El número complejo se escribe en términos de sus componentes real e imaginario, esto es:
.png)
Donde x es la componente real, y es la componente imaginaria y j es
, por definición.
Los signos están en función del cuadrante en el que se encuentra el número complejo. La siguiente aplicación te servirá para ubicar números complejos en el plano complejo.
Forma polar
En la forma polar, el número complejo se escribe en términos de su magnitud (módulo) y ángulo (argumento), esto es:
.png)
Donde r es la magnitud, f es el ángulo y e es la base del logaritmo natural, j es
por definición.
se usa con frecuencia
en lugar de
, por lo que la forma polar se escribe:
Debido a que podemos expresar un número complejo en ambas formas, es importante saber transformarlo de una forma a otra.
A continuación se muestra cómo pasar de una forma a la otra.
De polar a rectangular
entonces
.png)
De rectangular a polar
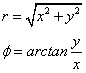
Con esta ecuación podemos encontrar el valor del ángulo, sin embargo, no podemos saber en qué cuadrante se encuentra. Este problema se puede resolver mediante una representación gráfica.
.png)