Con este recurso en particular se explicará el concepto de fasor y su uso dentro de los circuitos eléctricos.
An�lisis senoidal en estado estable
Fasores
El fasor es un número complejo que presenta información sobre la amplitud y el ángulo de fase de una función senoidal. El concepto del fasor se establece a partir de la identidad de Euler, la cual relaciona el exponencial de un número complejo con la función trigonómetrica (a veces llamada cis):
.png)
La función coseno es la parte real de la función exponencial, mientras que la función seno es la parte imaginaria. Considerado como número complejo, el exponencial tiene magnitud unitaria y su ángulo es f.
Por lo anterior, considerando que la frecuencia se mantiene constante, se considera al número complejo
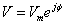
como la transformada fasorial de la señal senoidal
De esta forma, la transformada fasorial transfiere la función senoidal del dominio del tiempo al dominio de la frecuencia, lo cual permite que las operaciones de señales en el dominio del tiempo se realicen como operaciones con números complejos.
La expresión anterior es llamada forma polar del fasor. También podemos expresar el fasor en forma rectangular como:
Para comprender mejor el concepto de fasor, puedes abrir la siguiente aplicación, que te permite definir un fasor para observar la señal que representa.
La utlilización de fasores, permite que se pueda realizar una suma de señales senoidales de diferente fase, como una suma de números complejos.
Ejemplo:
Si
y
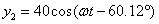
Expresa
como una sola función senoidal y obtén la solución utilizando el concepto de fasor.

Puedes utilizar la siguiente aplicación para practicar las operaciones basicas de señales, resueltas como fasores: