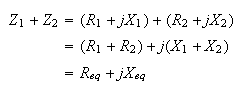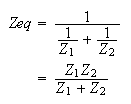Con este recurso en particular se mostrará al alumno el concepto de impedancia y admitancia, así como los arreglos entre ellas.
An�lisis senoidal en estado estable
Impedancia y admitancia
La ley de ohm V=IR aplicada en circuitos en CD, sirvió para definir la propiedad de resistencia. Para circuitos en AC, el concepto equivalente a resistencia es llamado impedancia (Z), expresado como la relación de la forma Z=V/I, donde el voltaje y la corriente se expresan en su valor efectivo rms. Para un circuito puramente resistivo R=Z.
La impedancia implica una parte real (resistencia, R) y una parte imaginaria (reactancia, X). Para desarrollar expresiones de la impedancia se utilizan los fasores dado que es fácil expresar señales de voltaje y corriente de AC como números complejos.
Podemos reducir arreglos de impedancias en serie y en paralelo de igual manera que se hace con las resistencias. La forma de obtener la impedancia equivalente conlleva las mismas operaciones, sólo se debe considerar que las operaciones se realizan con números complejos.
La admitancia es el recíproco de la impedancia
su unidad es el Siemens, en ocasiones llamado mho (ohm al revés). Se utiliza en los circuitos en paralelo para simplificar los cálculos, y en la solución de circuitos eléctricos por nodos.
La parte real, (G) se denomina conductancia y la parte imaginaria (B) susceptancia.
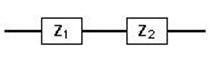
Impedancia en serie
Como se ve, en la fórmula para calcular una impedancia equivalente en serie, sumamos directamente los valores de las resistencias (parte real), y sumamos algebraicamente las reactancias, ya sean inductivas (+) o capacitivas (-).
Impedancia en paralelo
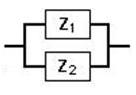
Para calcular la impedancia en paralelo requerimos de un mayor desarrollo, ya que se requiere realizar multiplicaciones y divisiones con números complejos; entonces tenemos dos opciones: utilizar la forma rectangular, o convertir a forma polar para simplificar el cálculo.
La herramienta que se presenta a continuación, te sirve para realizar cálculos de impedancias en serie y paralelo.