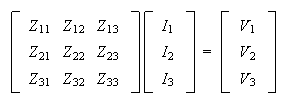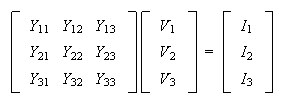An�lisis senoidal en estado estable

Mallas y nodos

Técnicas de análisis en corriente alterna

Para analizar circuitos CA se utilizan los mismos teoremas y técnicas que se vieron para circuitos CD, considerando que ahora se trabajará con números complejos. Sin embargo, el uso de divisores de voltaje y de corriente puede llevar a sistemas de ecuaciones bastante complejos, por lo que se sugiere utilizar los teoremas de Norton y Thévenin. Si contamos con valores de impedancias, se facilita el análisis por el método de mallas y, en caso, de tener valores de admitancias, es más viable el método de nodos.

Mallas y nodos

Ambos procedimientos se llevan a cabo tal y como se describieron para la solución de circuitos en corriente continua, sólo que ahora la matriz de resistencia del sistema corresponde a la matriz de impedancias para mallas, y de admitancias para nodos.

Para un circuito con tres mallas tendremos:

Para un circuito con tres nodos tendremos:

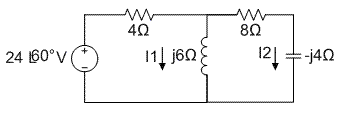
Ejemplo:
Encontrar las corrientes de malla I1 e I2

Malla 1

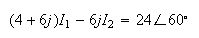
Malla 2

obtenemos el sistema:

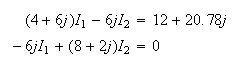
cuya solución es:

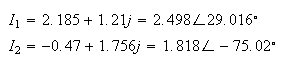
El ángulo de -75°, es con respecto al eje de los reales negativos; para que quede con respecto al eje positivo, se tiene: f = 180°-75° = 105°

Para resolver sistemas de ecuaciones con números complejos, se utiliza el mismo procedimiento que para los números reales, obviamente respetando las reglas de multiplicación de los complejos.