10. Un albañil acude a una tlapalería para comprar 2 kilos de cemento, contando con sólo $43.00. El dueño de la tlapalería le dice al albañil que tiene dos tipos de cemento: uno cuesta $26.00 y el otro $20.00. ¿Qué cantidad de cada cemento debe comprar el albañil para que el total de cemento sea 2 kilos y sólo gaste $43.00?

Solución

Para resolver este problema se proponen dos variables: x y y. La variable x representa la cantidad de cemento de $26.00 y la variable y representa la cantidad de cemento de $20.00.

Como la cantidad a comprar es dos kilos, la suma de las cantidades x y y de cemento debe sumar dos kilos. Esto puede representarse mediante la ecuación:

Por otra parte, sólo se cuenta con un presupuesto de $43.00, por lo que debe establecerse la ecuación:

 es lo que pagará por la cantidad de cemento de $26.00
es lo que pagará por la cantidad de cemento de $20.00

Tenemos entonces dos ecuaciones que deben resolverse en forma simultánea:

Para resolver el sistema de ecuaciones anterior, conviene multiplicar la primera ecuación por –26:

Con esta modificación se obtiene el sistema de ecuaciones:

Este sistema de ecuaciones tiene la ventaja de que si se suman las ecuaciones, se elimina la variable x: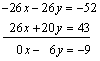

Obteniéndose una sola ecuación:

cuya solución es:

 

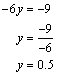
Para obtener el valor de x se sustituye en la primera ecuación el valor de y :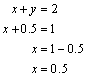

Por lo tanto, se debe comprar ½ kilo de cemento de $26.00 y 1.5 kilos de cemento de $20.00 para tener una mezcla de dos kilos por los que se pagarán $43.00.