Nombre |
Características |
Fórmula |
Media o promedio
para datos no
agrupados |
Es la más popular de las medidas de tendencia central; su cálculo es sencillo y útil para todo tipo de dato cuantitativo, siempre y cuando no haya datos extremos. |
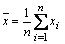
n es el número de datos. |
Media geométrica |
Es útil para promediar datos cuantitativos como porcentajes, índices, tasa de interés o tasa de crecimiento. |
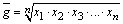
n es el número de datos. |
Media ponderada |
Es útil para promediar datos que no tienen todos el mismo peso o importancia. |
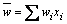
wi es el peso asociado al dato xi. |
Media armónica |
Esta medida se ocupa para promediar valores que representan rapidez, como velocidad, rendimiento y eficiencia.
Es necesario que todos los datos sean diferentes de cero. |
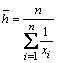
n es el número de datos. |
Media aritmética para
datos agrupados |
Cuando los datos están agrupados, la media se calcula con esta fórmula, la cual es útil para todo tipo de dato cuantitativo. |
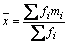
fi es la frecuencia de la clase i.
mi es la marca de la clase i. Esta marca se halla justo en medio de los valores extremos de la clase. |
Mediana |
Para calcular la mediana primero hay que ordenar los datos en forma ascendente. Después de ordenarlos, la mediana es el dato que se encuentra justo en medio de todos los datos.
Esta medida es adecuada para datos cuantitativos en los que pueden presentarse datos extremos. Si se presentan datos extremos, entonces éstos no influyen en la determinación de la mediana. |
Para ubicar el lugar donde se encuentra la mediana, una vez ordenados los datos en forma ascendente, se usa
Ubicación de la Md = 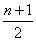
Md es la mediana.
n es el número de datos. |
Moda |
La moda de una muestra de datos es el dato de mayor frecuencia.
Es interesante notar que podría haber más de una moda.
Esta medida es útil para promediar datos cuantitativos. |
Para obtener la Moda (Mo) no se utiliza fórmula. Veamos un ejemplo:
2 4 5 3 7 2 6 4 2 9 4 1 2 4
En estos datos hay 2 modas: el 2 y el 4, ya que ambos se repiten el mismo número de veces (4). |