Ejemplo 1
Encuentra la información que se te pide:
Solución A. Para encontrar la media se aplica la fórmula: 
La muestra de este ejemplo es de 6 elementos, por lo que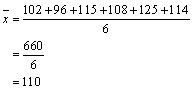 
B. El rango R es la diferencia entre el máximo valor de la muestra y el mínimo: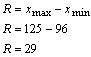 
C. Para encontrar la varianza hay que aplicar la fórmula: 
En donde Para facilitar los cálculos de la varianza será útil la siguiente tabla, en donde se calculan los términos
De la tabla anterior:  Entonces: 
Los datos de este ejemplo tienen una varianza de 106 D. Para calcular la desviación estándar s, aplico la fórmula: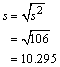 
Por lo tanto, la desviación estándar es 10.295 E. Para calcular el coeficiente de variación cv se aplica la siguiente fórmula: 
Para este caso se tiene el siguiente resultado: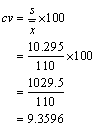 
El coeficiente de variación es de 9.36% F. Para calcular el índice de asimetría α3 se aplica la siguiente fórmula: 
Pero ya ha sido calculada la suma: 
Por otra parte, la desviación estándar es: 
De manera que: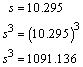 
Al introducir estos datos en el índice de asimetría se obtiene el siguiente resultado: 
El índice de asimetría es 0.055 Como G. Para calcular la Kurtosis 
De la tabla: 
Por otra parte, la desviación estándar es: 
De manera que: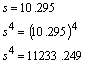 
Al introducir estos datos en la Kurtosis se obtiene el siguiente resultado: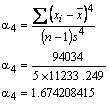 
El índice de Kurtosis es 1.67 Como |
. La media es:
es la media.
es sesgada a la derecha, esto significa que moda < mediana < media.
se aplica la siguiente fórmula:
, entonces la distribución es platicúrtica, esto significa que los datos están dispersos.