Ejemplo 4
Para la siguiente tabla de frecuencias encuentra:
A. Media. Solución A. Para una muestra de datos agrupados, la media se calcula con la siguiente fórmula: Para calcular las sumas de la fórmula anterior será útil desarrollar la siguiente tabla:
Con los datos obtenidos en la tabla anterior ya se puede calcular la media: 
La media para los datos agrupados es 24.84 B. Para una muestra de datos agrupados, la varianza s2 se calcula mediante la siguiente fórmula: Para facilitar los cálculos de la suma en la fórmula anterior será útil la siguiente tabla:
Con los datos obtenidos en la tabla anterior ya es posible obtener la varianza: 
C. El cálculo de la desviación estándar s es fácil, sólo hay que obtener la raíz cuadrada de la varianza: 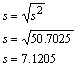
La desviación estándar es 7.12 |