Ejemplo 6

Los jugadores de futbol americano son jóvenes de peso muy variado, por ejemplo, un corredor de poder debe ser ligero para correr rápido; en cambio, los jugadores que están en la línea deben ser pesados para contener el embate de la línea ofensiva; los jugadores que regresan la patada no son ni muy pesados ni muy ligeros pues deben ser ágiles pero también requieren de fortaleza para proteger al corredor que trae el balón. La siguiente tabla de frecuencias contiene el peso de todos los jugadores de un equipo de futbol americano. Encuentra el peso promedio de los jugadores y la desviación estándar. Clase Intervalo kg Frecuencia 1 70 – 76 25 2 77 – 83 25 3 84 – 90 20 4 91 – 97 15 5 98 – 104 10 6 105 – 111 5 Solución Dado que la tabla contiene el peso de todos los jugadores, entonces se trata de una población y no de una muestra. El peso medio se calcula con la siguiente fórmula: Para facilitar el cálculo de la suma es conveniente desarrollar la siguiente tabla: Clase Intervalo kg Frecuencia Maraca de clase 1 70  - 76 25 2 77  - 83 25 80 2000 3 84 - 90 20 87 1740 4 91 - 97 15 94 1410 5 98 - 104 10 101 1010 6 105 - 111 5 108 540 Suma   100   8525 Con estos datos ya puede ser calculada la media: 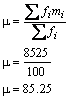El peso promedio de los jugadores es μ = 85.25 kg. Es un peso un poco ligero para la liga mayor. Para calcular la varianza σ2 se aplica la siguiente fórmula: Para facilitar el cálculo de la suma anterior es conveniente desarrollar la siguiente tabla: Clase Intervalo kg Frecuencia Maraca de clase 1 70 – 76 25 2 77 - 83 25 80 689.1 3 84 - 90 20 87 61.2 4 91 - 97 15 94 1148.4 5 98 - 104 10 101 2480.6 6 105 - 111 5 108 2587.8 Suma   100   10718.6 En la tabla anterior han sido calculadas las sumas de la fórmula de la varianza; al sustituir estos resultados en la fórmula se obtiene: La varianza es 107.186 Para calcular la desviación estándar σ hay que obtener la raíz cuadrada de la varianza: 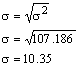La desviación estándar es 10.35, por ser diferente de cero significa que los datos están dispersos. El coeficiente de variación es: 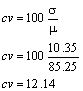Hay un 12.14 % de variación en los datos.