El fin de esta actividad es presentar el tema de velocidad media e instantánea, se indica revisar algunos objetos java que ejemplifican las definiciones.
Movimiento rectilíneo
Velocidad media e instantánea
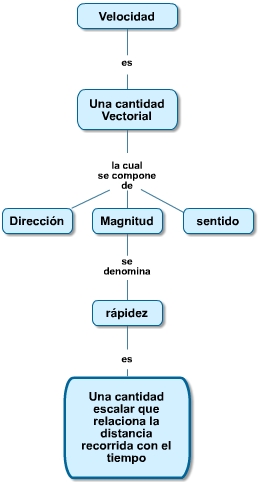
En el lenguaje coloquial los términos velocidad y rapidez son prácticamente sinónimos, pero en el lenguaje científico son diferentes, como se puede apreciar en el siguiente mapa conceptual:
|
Definición
Cuando una partícula se mueve cambia de posición y emplea un intervalo de tiempo en realizar este cambio; a un tiempo 1 la partícula se encuentra en una posición 
y a un tiempo 2 la partícula está ahora en una posición 
, podemos definir la velocidad promedio como el cambio de posición 
en el intervalo de tiempo 
.
Como lo vimos anteriormente, una partícula
se puede desplazar una distancia en
un intervalo de tiempo . Entonces la
velocidad media de la partícula en el intervalo de tiempo se expresa como:
¿Qué sucede si disminuimos el intervalo de tiempo a magnitudes muy pequeñas?, por ejemplo, cuando tiende a cero. Podemos resolver esta pregunta haciendo la siguiente consideración:
Al calcular el límite de la expresión anterior se obtiene:
Este límite es la derivada de la posición con respecto al tiempo, el cual nos define la velocidad en un instante de tiempo y su expresión es:
Lo que significa que podemos conocer la velocidad instantánea derivando una función que describa la posición con respecto al tiempo.
Consulta la aplicación Velocidades media e instantánea © 2004 Pearson Educación S.A., que se muestra en la siguiente imagen:
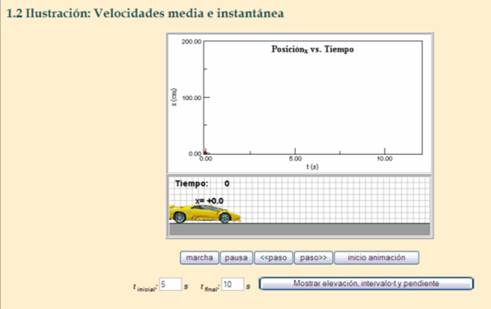
En esta página se encuentra un objeto java que muestra la gráfica de posición contra tiempo de un automóvil que se mueve con aceleración constante. El recurso permite determinar la velocidad media en un intervalo de tiempo. Para trabajar con la simulación hay que hacer lo siguiente:
1. Hay dos espacios vacíos para el tiempo inicial y el tiempo final, recuerda que tiempo inicial debe se mayor o igual a cero; considera un tiempo final menor o igual a 10 para que puedas ver la gráfica completa.
2. Observa cómo se dibuja la gráfica posición contra tiempo. ¿Qué tipo de gráfica es?
a) Lineal.
b) Polinomio de orden "n"
3. Da click en el botón mostrar elevación, intervalo-t y pendiente.
4. Calcula la pendiente de la línea azul con la siguiente ecuación:
¿Puedes decir con qué otro nombre conocemos está pendiente?
5. Realiza los pasos del 1 al 5 varias veces pero cambiando (
) y (
) en sus respectivas casillas.
Haciendo más pequeño el intervalo entre () y () , observa que pasa con la pendiente de la línea azul. Puedes utilizar los
datos de la siguiente tabla:
|
|
0 |
10 |
2 |
8 |
4 |
6 |
5.9 |
6 |
A la pendiente de esta línea se le conoce como velocidad media cuando el intervalo está entre dos puntos cualesquiera. De forma gráfica se aprecia de la siguiente forma:
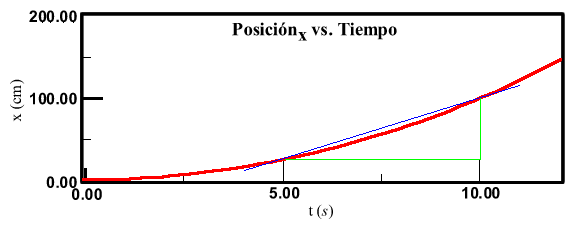
La velocidad media es la pendiente de la línea azul.
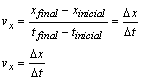
es la velocidad en la dirección x.
es la coordenada x al final del movimiento. 
es la coordenada x al inicio del movimiento. 
es el tiempo que tarda el cuerpo en estar en la posición x al final.
es el tiempo inicial. Toma en cuenta que si 
es mayor a cero, la velocidad promedio también es mayor a cero, si 
es menor a cero, la velocidad media es menor a cero, lo que significa que tendra un valor negativo. El signo de la velocidad nos está indicando el sentido hacia dónde se mueve una partícula. Recuerda que por convención consideramos a la derecha del origen como positivo. A esta división 
se le conoce también como razón de cambio de la posición con respecto al tiempo.
Al tomar el límite cuando 
tiende a cero obtenemos:
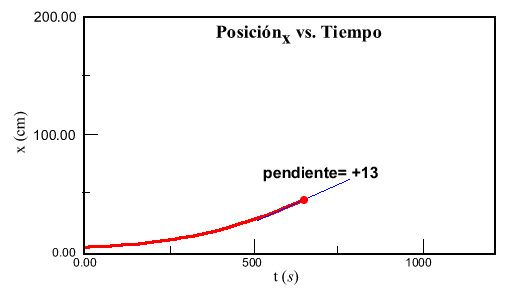
En esta figura se aprecia el valor de la velocidad como la pendiente de la recta tangente (la recta se muestra en línea azul) a la gráfica de la posición respecto del tiempo.
Para observar en movimiento la grafica anterior de la velocidad
instantánea consulta la aplicación Velocidades media e instantánea © 2004 Pearson Educación S.A., selecciona
el botón 
seguido del
botón 
que aparecen en la parte inferior y
observa la animación.
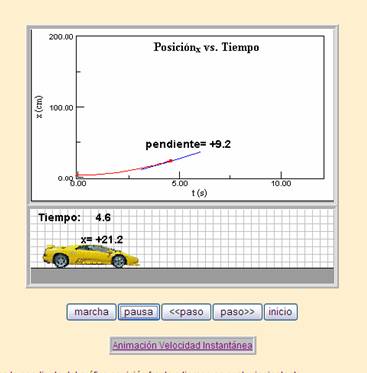
Con este análisis ya tenemos la ecuación para la velocidad instantánea:
Problema: Consulta la aplicación Gráfico posición vs. tiempo para el coche de juguete © 2004 Pearson Educación S.A.
-
Espera que se termine de cargar la animación.
Presiona el botón animación 1 y observa el gráfico detenidamente, puedes poner pausa y llevar el puntero del ratón sobre el gráfico; haz click sobre la gráfica o sobre el coche y mientras dejas apretado el botón izquierdo podrás ver las coordenadas de posición x y tiempo t y compararlas con las coordenadas del punto rojo sobre el coche. Para observar si coinciden o no presiona "marcha", sigue el movimiento del coche y su gráfica, puedes poner pausa y comparar las coordenadas del coche y de la gráfica cuantas veces quieras.
-
Realiza lo mismo que el paso anterior pero para las animaciones 2, 3 y 4.
Revisa el siguiente documento en el que encontrarás:
Ejemplos, problemas resueltos y propuestas de problemas.