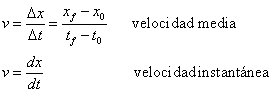Movimiento en un plano

Velocidad y aceleración media e instantánea

I. Introducción En la unidad anterior se estudió el movimiento rectilíneo, este tipo de movimiento se realiza sobre el eje x, por lo que es un movimiento unidimensional, vimos también que son muchos los fenómenos que se caracterizan por este tipo de movimiento. En la presente unidad estudiaremos el movimiento en un plano, este movimiento está caracterizado por que la posición, velocidad y aceleración de un cuerpo en movimiento están determinados por vectores, de tal manera que la posición del cuerpo tiene componentes rectangulares "x","y". Además, para cada componente tendremos diferentes tipos de movimiento. Son muchos los fenómenos naturales cuyo movimiento está constreñido en un plano, por ejemplo, la orbita terrestre es una elipse, la cual es una figura plana, el movimiento de un proyectil es una parábola, misma que también es una figura plana, el mapa de la guia roji es un documento en donde se ubican las coordenadas de cualquier lugar que sea necesario ubicar, y este documento es un plano en donde la ubicación de un punto está determinada por un vector de posición con coordenadas bien establecidas. 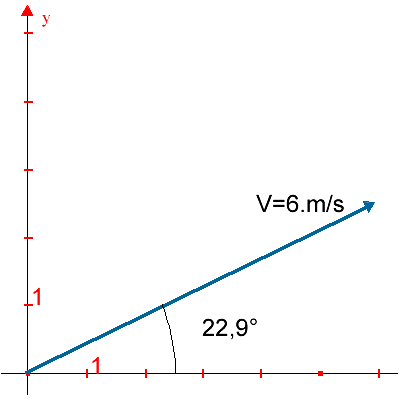En la unidad 1 se estudiaron las ecuaciones de velocidad media y velocidad instantánea las cuales damos a continuación: Estas ecuaciones serán de utilidad para el estudio de movimiento en un plano. Considera una partícula cuyo movimiento está constreñido a un plano, para este tipo de movimiento surge la necesidad de calcular las componentes rectangulares (x, y) de los vectores de posición, velocidad y aceleración. En geometría analítica realizaste la descomposición vectorial para los vectores de posición, en el siguiente ejercicio calcularás las componentes rectangulares de un vector de velocidad, y la manera de hacerlo es la misma que para el vector de posición. Ejercicio La siguiente figura muestra el vector de velocidad de una partícula. Calcula las componentes rectangulares de este vector.

 

Respuesta

II. Simulación de la situación

Para fortalecer el concepto de vector y sus componentes es recomendable llevar a cabo la siguiente simulación en la que es posible manipular los parámetros relacionados a un vector.

Es importante tomar en cuenta las siguientes indicaciones para el desarrollo del ejercicio:

• Mueve la punta del vector con el ratón y observa qué pasa con las coordenadas x y y, la magnitud R del vector y su ángulo.

• Observa además los componentes (la línea azul y la roja) y mira qué sucede con los vectores x y y.

III. Análisis de la velocidad en diferentes sistemas de referencia

La velocidad media y la velocidad instantánea de un objeto que se desplaza en el plano se puede analizar desde los siguientes sistemas de referencia:

• Sistema de referencia en coordenadas rectangulares.

• Sistema de referencia en componentes normal y tangencial a la trayectoria.

• Sistema radial transversal.

En esta sección aplicaremos el sistema de referencia en coordenadas rectangulares para analizar el movimiento de un proyectil; y aplicaremos el sistema de referencia en coordenadas normal y tangencial para analizar el movimiento circular.

Consideremos el siguiente vector r:

En donde:
 es el vector de posición en el plano.
x es la componente X del vector.
y es la componente Y del vector.

es el vector unitario en la dirección del eje X.

es el vector unitario en la dirección del eje Y.

En general, cualquier vector, ya sea de posición, velocidad o aceleración está constituido por sus componentes x y y como se muestra en la figura anterior, en donde se aprecia tanto el vector de posición r como el de velocidad v. Las componentes del vector velocidad pueden ser analizadas en forma independiente para deducir las ecuaciones de velocidad instantánea de un cuerpo:

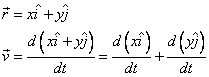
Entonces:

Si el sistema de referencia no fuera inercial tendríamos que derivar los vectores unitarios con respecto al tiempo de la siguiente manera (sólo se va expresar en el eje X, en el eje Y sería el mismo procedimiento):

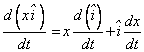
Si consideramos un sistema de referencia inercial, entonces la derivada del vector unitario i sería cero, ya que este vector es constante en un sistema de referencia inercial. Considerando unicamente sistemas de referencia inercial, la derivada de la posición x respecto del tiempo es:

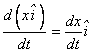
De donde se obtiene las relaciones para la velocidad:

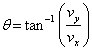
es la velocidad instantánea en el eje x en el instante de tiempo t.

es la velocidad instantánea en el eje y en el instante de tiempo t.

es la magnitud del vector velocidad.

es el ángulo del vector velocidad con respecto al eje x (en este caso).

�

 

Las ecuaciones de la velocidad instantánea que hemos encontrado serán usadas para deducir las ecuaciones de la aceleración instantánea:

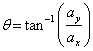
es la aceleración instantánea en el eje x en el instante de tiempo t.

es la aceleración instantánea en el eje y en el instante de tiempo t.

es la magnitud del vector aceleración.

es el ángulo del vector aceleración con respecto al eje x (en este caso).

Velocidad y aceleración media.

Las componentes de la velocidad media son:

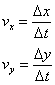
es la velocidad media en el eje X

es la velocidad media en el eje Y

 

Éstas son las componentes del vector velocidad:

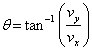
es el vector velocidad instantánea de la partícula en el instante de tiempo t.

es la velocidad instantánea en el eje x en el instante de tiempo t.

es la velocidad instantánea en el eje y en el instante de tiempo t.

es la magnitud del vector velocidad.

es el ángulo del vector velocidad con respecto al eje x (en este caso).

Recordemos que la diferencia es cómo se calculó la velocidad.

Las componentes de la aceleración media son:

                                   

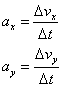
es la velocidad media en el eje X.

es la velocidad media en el eje Y.

Éstas son las componentes del vector aceleración:

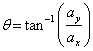
es la aceleración instantánea en el eje x en el instante de tiempo t.

es la aceleración instantánea en el eje y en el instante de tiempo t.

es la magnitud del vector aceleración.

es el ángulo del vector aceleración con respecto al eje x (en este caso).

Recordemos que la diferencia es cómo se calculó la aceleración.