Movimiento en un plano

Movimiento circular

I. Antecedentes Cuando vas a un parque de diversiones, ¿has observado que la mayoría de los juegos mecánicos se mueven en una trayectoria circular?, cuando te subes a estos juegos experimentas aceleraciones, las cuales sientes como fuerzas en diferentes partes de tu cuerpo. Las siguientes preguntas evocan tus recuerdos sobre este tipo de movimiento (si no recuerdas ¡ve al parque de juegos mecánicos!), y tienen la finalidad de relacionar tu experiencia en ellos, con la teoría del presente tema. Supongamos que te subes a un juego que se mueve en un trayectoria circular horizontal, tal y como se muestra en la figura. Selecciona las siguientes preguntas y respóndelas con cuidado:

Preguntas

De la sección anterior (tiro parabólico) sabemos que:

La velocidad media e instantánea de un objeto que se desplaza en el plano se puede analizar desde diferentes sistemas de referencia:

• Sistema de coordenadas rectangulares.

• Sistema en componentes normal y tangencial a la trayectoria.

• Sistema radial transversal.

En esta sección ocuparemos el sistema de referencia en coordenadas normal y tangencial ya que es el más adecuado para analizar el movimiento circular.

En la sección anterior (tiro parabólico) el análisis de movimiento se desarrolló sobre el sistema de referencia en coordenadas rectangulares cuyo conjunto de variables son x, y. En el problema del juego mecánico, el carrito sigue una trayectoria circular como se muestra en la siguiente figura:

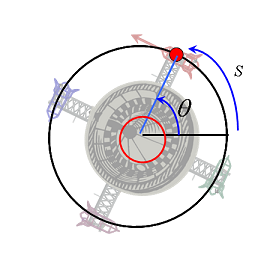
De esta imagen apreciamos que el desplazamiento s es sobre la trayectoria circular, y la podemos calcular con la expresión:

s = Rθ

En donde:

R: es el radio de la circunferencia.

θ : es el ángulo generado por el movimiento del carrito.

Por otra parte, sabemos que la velocidad tiene la siguiente expresión:

Al sustituir s = Rθ se obtiene la siguiente expresión:

Como la trayectoria es una circunferencia, entonces el radio R es constante, por lo que el radio queda fuera de la derivada:

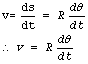
Se define la velocidad angular como:

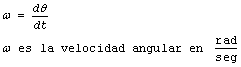
Entonces la velocidad v se relaciona con la velocidad angular por la siguiente expresión:

v = Rω

 

En la animación se aprecia que la velocidad es tangente al movimiento en cualquiera de las posiciones mostradas; por esta razón, a la velocidad en este tipo de movimiento se le denomina velocidad tangencial.

Para calcular la aceleración del carrito del juego mecánico se calcula la siguiente derivada:

 

A este tipo de aceleración se le denomina aceleración tangencial, y como su nombre lo dice, ésta es tangente a la trayectoria circular. Ahora podemos relacionar este concepto con la pregunta 3. La aceleración tangencial es la que sentimos como "la fuerza" que nos empuja al empezar el movimiento del carrito.

A partir de las preguntas 1 y 2 sabemos que hay una fuerza que nos mantiene dentro del carrito, cuando la trayectoria de éste es circular, y también que ésta tiene una dirección radial con sentido hacia el centro de la circunferencia; esta fuerza es la causa de una aceleración que tiene la misma dirección y sentido, que la fuerza que sentimos al estar dentro del carrito en movimiento; a esta aceleración se le denomina aceleración normal y se calcula con la siguiente expresión matemática:

La figura anterior muestra el vector aceleración así como sus componentes normal y tangencial. La magnitud de la aceleración se calcula con la siguiente fórmula

II. Simulación M.C.U.

Desarrolla la simulación Movimiento circular uniforme y aceleración © 2004 Pearson Educación S. A.

Sigue las instrucciones que se indican en el sitio y verifica lo que has aprendido en relación al movimiento circular uniforme.

III. Ecuaciones del M.C.U.

Escribamos juntas las ecuaciones:

 θ: posición angular.
Velocidad angular.
Aceleración angular.

El siguiente cuadro muestra las ecuaciones para el movimiento angular, en las que la velocidad angular y la aceleración angular son constantes.

 

Ecuaciones para cuando la aceleración angular 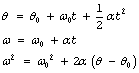 es constante.

Ecuaciones para cuando la velocidad angular  es constante.