Procedimiento para el análisis de problemas
PROCEDIMIENTO PARA EL ANÁLISIS (pp. 98-99, Hibbeler, Ingeniería mecánica dinámica, Prentice Hall)
Las ecuaciones de movimiento se emplean para resolver los problemas que requieren una relación entre las fuerzas que actúan sobre una partícula y el movimiento acelerado que provocan. Siempre que sean aplicadas es preciso identificar las componentes desconocidas de las fuerzas y la aceleración, y escribir un número equivalente de ecuaciones. Si son necesarias más ecuaciones para encontrar la solución, es conveniente considerar la cinemática.
Diagrama de cuerpo libre
-
Seleccione el sistema de coordenadas inerciales. Con frecuencia, se elige las coordenadas rectangulares
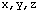para analizar problemas en los que la partícula tiene un movimiento rectilíneo. Si esto ocurre, es preciso extender uno de los ejes en dirección del movimiento. -
Una vez que se ha establecido las coordenadas, dibuje el diagrama de cuerpo libre de la partícula. Esto es muy importante, ya que se trata de una representación gráfica de todas las fuerzas que actúan sobre la partícula y por lo tanto permite descomponer estas fuerzas en sus componentes en
. -
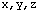Es preciso establecer también la dirección y sentido de la aceleración de la partícula. Si se desconoce el sentido de estas componentes, por conveniencia matemática suponga que se encuentra en la misma dirección que los ejes positivos de las coordenadas inerciales. Es posible trazar la aceleración en el sistema de coordenadas
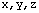, pero no sobre el diagrama de cuerpo libre, o bien, representarla como el vector 
en el diagrama cinético. -
Una vez constituido el diagrama de cuerpo libre, identifique las incógnitas.
Ecuaciones de movimiento
-
Si es posible descomponer las fuerzas directamente a partir del diagrama de cuerpo libre, aplique las ecuaciones de movimiento en su forma de componentes escalares. Si la geometría del problema parece ser complicada (lo que ocurre muchas veces en el caso de tres dimensiones) es posible utilizar para la solución el análisis cartesiano de vectores.
Fricción
-
Si la partícula está en contacto con una superficie áspera, quizá sea necesario utilizar la ecuación de fricción, la cual relaciona el coeficiente de fricción cinético
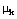con las magnitudes de las fuerzas normales y de fricción 
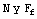, que actúan sobre el diagrama de cuerpo libre de tal forma que se opone al movimiento de la partícula en relación con la superficie con la que está en contacto.
Resorte
-
Si la partícula está conectada a un resorte elástico cuya masa es despreciable, es posible relacionar la fuerza
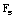del resorte con la deformación del resorte por medio de la ecuación 
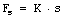. Donde 
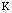es la rigidez del resorte medida como una fuerza por unidad de longitud, y 
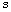es el alargamiento o compresión que se deforma como la diferencia entre la longitud deformada 
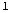y la longitud no deformada 
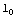, es decir, 
.
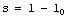Cinemática
-
Como se estableció con anterioridad, si no es posible obtener una solución completa de manera estricta a partir de la ecuación de movimiento, se podría considerar las ecuaciones de cinemática. Por ejemplo, si se ha de calcular la velocidad o la posición de la partícula, será necesario aplicar las ecuaciones cinemáticas adecuadas una vez que se determine la aceleración de dicha partícula a partir de
.
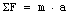Si la aceleración es una función del tiempo, utilice 
y 
las que, cuando se integran, proporcionan la velocidad y posición de la partícula.
Si la aceleración es una función del desplazamiento, integre 
para obtener la velocidad como una función de la posición.
Si la aceleración es constante, use
para determinar la velocidad o posición de la partícula.
En todos los casos, asegúrese de que las direcciones positivas de las coordenadas inerciales utilizadas para escribir las ecuaciones cinemáticas son las mismas que se emplean para escribir las ecuaciones de movimiento; de no ser así, la descomposición de un vector desconocido en sus componentes produce un escalar negativo, e indica que la componente actúa en dirección opuesta a aquella que se opuso.