Con este objeto de aprendizaje el alumno relacionará los conceptos de impulso y momento lineal, estudiados anteriormente, con los fenómenos de choques y colisiones.
Impulso y momento lineal
Choques y colisiones
I. Introducción Cuando dos objetos, como un martillo y un clavo, un palo de golf y una pelota, o incluso dos automóviles, están en contacto por un corto periodo, pueden ejercer grandes fuerzas uno sobre el otro, de tal forma que las fuerzas externas se pueden despreciar. A este tipo de situaciones se les conoce como choque, colisión o impacto. Para analizar los choques y colisiones primero tenemos que revisar el tema de conservación del impulso y momento lineal.
II. Conservación del momento lineal Consideremos un sistema dinámico compuesto por varios cuerpos en movimiento. Supongamos además que sobre este sistema de cuerpos en movimiento no existen fuerzas externas aplicadas al sistema; entonces el momento lineal del sistema se conserva, es decir, permanece constante mientras no haya alguna fuerza que interactúe en el sistema de cuerpos. |
La ley de conservación del momento, al igual que la de conservación de la energía, es una ley básica en física y ambas son necesarias para el estudio de muchos problemas de aplicación.
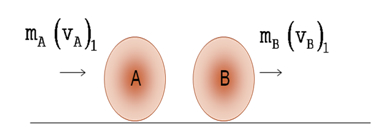
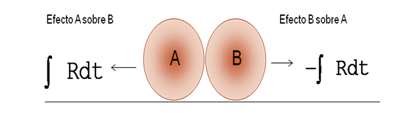
Para deducir las fórmulas de aplicación en problemas de colisiones consideremos un sistema dinámico, formado únicamente por dos cuerpos en movimiento (vea la siguiente figura para tener una representación gráfica del sistema propuesto). Sean mA, vA la masa y velocidad del cuerpo A, y sean mB, vB la masa y la velocidad del cuerpo B. Supongamos también que sobre este sistema no actúa fuerza externa alguna; entonces, cuando los cuerpos A y B colisionan, se tienen fuerzas FAB y FBA que actúan sobre los cuerpos.
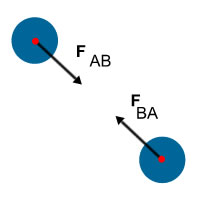
Si 
es la fuerza que ejerce el cuerpo A sobre el cuerpo B, entonces 
es la fuerza que ejerce el cuerpo B sobre el cuerpo A, ya sea por contacto directo o por un resorte que los conecte.
La tercera ley de Newton establece que la fuerza es igual y opuesta a la fuerza , por lo que:
Al aplicar el concepto de impulso y cantidad de movimiento a cada cuerpo se obtienen las siguientes ecuaciones:
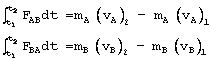
Al restarlas se obtiene:
La ecuación anterior implica que la cantidad de movimiento lineal del sistema de masas A y B se conserva, es decir:
Para determinar el centro de masa del sistema de dos cuerpos es necesario un sistema de referencia respecto del cual hacer mediciones. Considera un sistema de referencia en el que el vector rA sea el vector de posición del cuerpo A, y rB el vector de posición del cuerpo B, como se muestra en la siguiente figura:
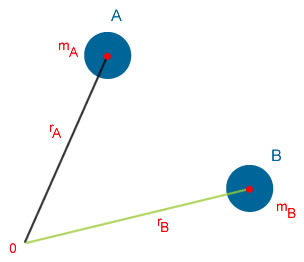
Sea r la coordenada del centro de masa del sistema de dos cuerpos; entonces:
Donde 
es la velocidad del centro de masa del sistema, y el término
constante
En forma general:
Choque elástico e inelástico
Apliquemos el resultado anterior al problema de un choque entre dos cuerpos que ocurre durante un intervalo pequeño de tiempo, en el cual los dos cuerpos ejercen entre sí fuerzas relativamente grandes. A este tipo de choque se le llama impacto.
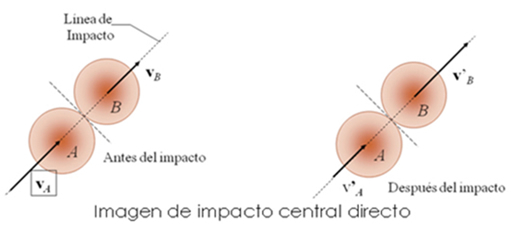
Si las velocidades de los dos cuerpos están dirigidas a lo largo de la línea de impacto, se dice que el impacto es directo, pero si uno o ambos cuerpos se mueven en líneas diferentes, entonces se trata de un impacto oblicuo, como el que se muestra en la siguiente figura:
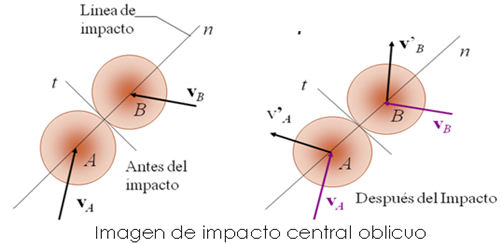
Impacto central directo
Analicemos ahora el impacto central directo y consideremos que las masas de los cuerpos A y B son diferentes, aunque se mueven sobre la misma línea y en la misma dirección (como se muestra en la figura). Entonces se tienen los siguientes resultados:
1. Si 
, la partícula A golpea a la partícula B.
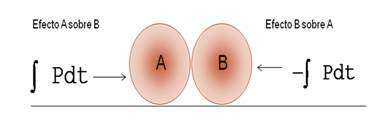
2. Durante la colisión los cuerpos se deforman, de forma tal que hay un impulso 
sobre cada cuerpo; además este impulso es igual y de sentido opuesto para cada cuerpo.
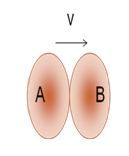
3. Sólo en el instante de máxima deformación ambas partículas se desplazan con una velocidad común v.
4. Después del periodo de restitución, en el cual las partículas recuperan su forma original o bien permanecen deformadas, el impulso de restitución 
es igual, pero opuesto para cada cuerpo; además, los cuerpos se separarán.
* En realidad, las propiedades físicas son tales que 
5. Después de la separación:
Debido a la ley de conservación del momento, se tiene el siguiente resultado:
Para determinar las velocidades 
necesitamos considerar el impulso durante las fases de deformación y de restitución del impacto.
La relación entre el impulso de restitución e impulso de deformación se conoce como coeficiente de restitución e:
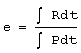
Para el cuerpo A el coeficiente de restitución es:
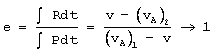
Para el cuerpo B es:
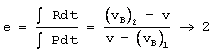
Eliminando la incógnita 
de (1) y (2) es posible expresar el coeficiente de restitución como:
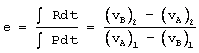
Las siguientes dos ecuaciones son utilizadas para determinar la velocidad de cada partícula después del impacto:
----------------Fórmula (1) 
------------------Fórmula (2)
En general e tiene un valor entre 0 y 1:
Si e = 1, se trata de un impacto elástico.
Si e = 0, se trata de un impacto totalmente inelástico.
.Impacto elástico 
Si la colisión entre ambas partículas es perfectamente elástica:
De la fórmula (2) se tiene 
En la ecuación anterior colocamos las velocidades del cuerpo A del lado izquierdo de la igualdad y las del cuerpo B del lado derecho para obtener:
.gif){kind=small}
--------------Fórmula (3)
Y en la fórmula (1) colocamos las velocidades del cuerpo A del lado izquierdo de la igualdad y las del cuerpo B del lado derecho para obtener:
-------------Fórmula (4)
Si multiplicamos los elementos del lado izquierdo de las fórmulas (3) y (4), hacemos lo mismo para los términos del lado derecho de la igualdad y obtenemos:
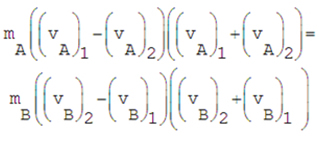
Desarrollando esta ecuación obtenemos:
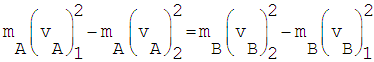
La ecuación anterior se puede reescribir de la siguiente manera:
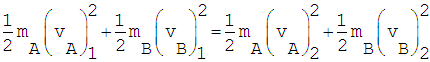
Esta ecuación establece que en un impacto totalmente elástico, la energía cinética del sistema de dos cuerpos se conserva.
Impacto plástico o totalmente inelástico (e = 0)
Este tipo de impacto ocurre cuando, después de la colisión, los cuerpos se acoplan o quedan pegados formando un sólo cuerpo. Después de la colisión, ambos cuerpos, al estar pegados, se mueven con la misma velocidad.
Si e = 0, entonces:
Sea 
a la velocidad de ambos cuerpos unidos
después de la colisión, es decir:
Entonces, la ecuación de conservación del momento lineal queda de la siguiente forma:
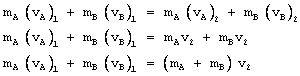
La última ecuación se utiliza cuando la colisión es totalmente inelástica.
Te recomendamos que realices la actividad de aprendizaje que se encuentra en la siguiente liga:
Una colisión elástica © 2004 Pearson Educación S.A.
En ella podrás observar el comportamiento del impacto elástico cambiando los parámetros de velocidad de los cuerpos que chocan.
III. Ejemplo resuelto
Para que comprendas mejor la forma de utilizar estos conceptos, selecciona el siguiente vínculo que contiene el video de un ejemplo resuelto.
IV. Problema propuesto
Selecciona el siguiente vínculo para descargar un ejercicio y pon en práctica tus conocimientos.