Con este objeto de aprendizaje, el alumno recordará el tema centro de masa estudiado anteriormente en estática.
Impulso y momento lineal
Centro de masa
El centro de gravedad es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas masas materiales de un cuerpo. En otras palabras, el centro de gravedad de un cuerpo es el punto de aplicación de la resultante de todas las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo.
El estudio del problema de movimiento de un sistema de partículas sometido a fuerzas externas requiere del concepto de centro de masa, el cual se presenta enseguida:
El centro de masa de un sistema, es el punto geométrico que dinámicamente se comporta como si estuviese sometido a la resultante de las fuerzas externas al sistema.
Al encontrar la posición de este punto para un sistema de partículas, se debe considerar el promedio de la masa de cada partícula. De esta manera, el centro de masa se determina con las siguientes expresiones:
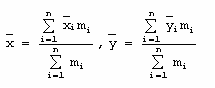
En general, el centro de gravedad y el centro de masa para un sistema de partículas no coinciden. Esto se debe a que el peso de cada partícula depende de su distancia al centro de la tierra, una consecuencia de la ley de gravitación universal de Newton. Además, las fuerzas gravitacionales están dirigidas a este mismo punto, y por consiguiente las líneas de acción de estas fuerzas no son realmente paralelas. Sin embargo, para algunos fines prácticos estas variaciones son de poca importancia y generalmente no son consideradas, lo que conduce a que el centro de masa sea igual al centro de gravedad.
Las siguientes expresiones determinan las coordenadas del centro de gravedad de un sistema de partículas:
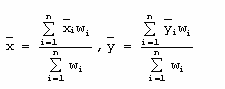
Si consideramos que la fuerza gravitacional es constante para todas las partículas que forman el sistema, entonces de las ecuaciones anteriores se deriva lo siguiente:
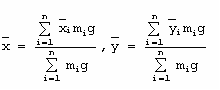
En donde se ha sustituido w por mg. Al factorizar g en las ecuaciones anteriores se obtiene: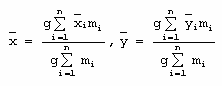 
Y como 
, entonces se tiene el siguiente resultado:
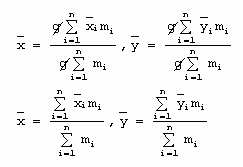
Estas ecuaciones son las mismas que las del centro de masa, y este resultado es así porque hemos considerado que la fuerza gravitacional es constante, y es la misma para cada partícula del sistema.
A continuación se da lo que representa cada variable:
es la coordenada x del centro de masa de todo el sistema de partículas.
es la coordenada x de la i-esima partícula dentro del sistema de partículas analizado.
es la coordenada y del centro de masa de todo el sistema de partículas.
es la coordenada y de la i-esima partícula dentro del sistema de partículas analizado.
Ejemplo resuelto
Para que comprendas mejor la forma de utilizar estos conceptos, selecciona el siguiente vínculo que contiene un ejemplo resuelto.
Problema propuesto
Selecciona el siguiente vínculo para descargar un ejercicio y poner en práctica tus conocimientos.