Con este objeto de aprendizaje se retoma el concepto de momento de una fuerza, visto con antelación en la asignatura de estática
Equilibrio, momento de una fuerza
Momento de una fuerza
I. Introducción Cuando abrimos o cerramos la llave de la regadera, cuando apretamos un tornillo, para girar la llave que da marcha al coche, aplicamos un momento para lograr un giro y, por la experiencia adquirida, sabemos que entre más lejos estemos del punto sobre el cual queremos hacer girar el objeto, es más fácil lograrlo. En el análisis que sigue se podrá saber el porqué de esta apreciación práctica y qué relación tiene esta distancia con la fuerza aplicada para lograr que la pieza que queremos mover gire. En esta unidad se estudia el momento de una fuerza. Un ejemplo de aplicación práctica es el que se muestra en el taladro de mano de la siguiente figura:
En el taladro de mano se tiene que aplicar un momento, como lo indica la flecha roja, para que la broca gire. Éste es el antecesor del moderno taladro eléctrico el cual, con su motor, es capaz de desarrollar un momento más grande que el que podemos desarrollar nosotros usando la fuerza de nuestra mano. ¡Increíble! cómo por medio de los engranes podemos transformar un momento en un eje, en una máquina para perforar.
|
II. Momento de una fuerza
Supongamos que tenemos un cuerpo rígido sobre el cual se aplica una fuerza, como se aprecia en la siguiente animación:
En esta animación se aprecia que, al mismo tiempo que se desplaza el cuerpo, también gira, haciendo necesario que la suma de fuerzas sobre él sea cero, para que el cuerpo esté en equilibrio de translación. Esta condición es suficiente para que el cuerpo no se desplace pero la condición no impide que el cuerpo gire. Para que el cuerpo no gire al aplicarle la fuerza debe hacerse una restricción adicional, debe exigirse que la suma de los momentos de cada fuerza sea cero. El momento de una fuerza es un concepto que permite determinar en qué medida un cuerpo rígido tiende a girar al aplicarle un conjunto de fuerzas. La forma analítica del momento de una fuerza involucra el producto cruz de dos vectores, el cual analizamos a continuación.
III. Producto cruz
El producto cruz entre los vectores ![]() y
y ![]() da por resultado un vector
da por resultado un vector ![]() . Este producto se denota de la siguiente manera:
. Este producto se denota de la siguiente manera:
y se lee como: “![]() es igual a
es igual a ![]() cruz
cruz ![]() ”.
”.
Magnitud. La magnitud del vector ![]() se define como el producto de las magnitudes de los dos vectores
se define como el producto de las magnitudes de los dos vectores ![]() y
y ![]() y el seno del ángulo θ entre los vectores:
y el seno del ángulo θ entre los vectores: ![]() .
.
Dirección. la dirección del vector ![]() es perpendicular al plano que contiene los dos vectores
es perpendicular al plano que contiene los dos vectores ![]() y
y ![]() , además, los vectores
, además, los vectores ![]() ,
, ![]() y
y ![]() forman un sistema derecho; es decir, la dirección de
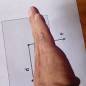
forman un sistema derecho; es decir, la dirección de ![]() se especifica por la regla de la mano derecha. Para encontrar la dirección de
se especifica por la regla de la mano derecha. Para encontrar la dirección de ![]() aplicando la regla de la mano derecha, hay que doblar los dedos de la mano derecha desde el vector
aplicando la regla de la mano derecha, hay que doblar los dedos de la mano derecha desde el vector ![]() (cruz) hacia el vector
(cruz) hacia el vector ![]() . El pulgar apunta entonces en la dirección de
. El pulgar apunta entonces en la dirección de ![]() , como se muestra en la siguiente figura:
, como se muestra en la siguiente figura:
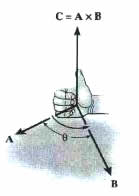
Si conocemos la magnitud y la dirección de ![]() , entonces el producto cruz lo podemos escribir de la siguiente manera:
, entonces el producto cruz lo podemos escribir de la siguiente manera:
Donde el escalar ![]() representa la magnitud de
representa la magnitud de ![]() y el vector unitario
y el vector unitario ![]() indica la dirección de
indica la dirección de ![]() . Los términos de la ecuación anterior están ilustrados en la siguiente figura:
. Los términos de la ecuación anterior están ilustrados en la siguiente figura:
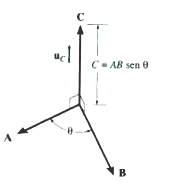
Si ambos vectores ![]() y
y ![]() son diferentes de cero y si aún asíi el producto cruz
son diferentes de cero y si aún asíi el producto cruz ![]() , entonces:
, entonces: ![]() esto sucede cuando:
esto sucede cuando: ![]() . Lo cual significa que
. Lo cual significa que ![]() es paralelo a
es paralelo a ![]() .
.
IV. Momento de una fuerza
Forma escalar. Los conceptos que tratan el momento de una fuerza pueden ilustrarse con un ejemplo sencillo. Consideremos la fuerza ![]() aplicada al extremo de una llave stillson:
aplicada al extremo de una llave stillson:
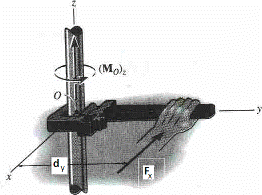
El efecto de esta fuerza es producir un giro al tubo alrededor del eje z. La experiencia enseña que para producir un giro más eficientemente la fuerza ![]() debe aplicarse de tal manera que se forme un ángulo recto entre la fuerza y la empuñadura de la llave, además la distancia
debe aplicarse de tal manera que se forme un ángulo recto entre la fuerza y la empuñadura de la llave, además la distancia ![]() debe ser tan grande como sea posible. Este efecto rotacional de una fuerza alrededor del eje z se llama algunas veces torque, pero con mayor frecuencia se le llama momento de una fuerza o, simplemente, momento
debe ser tan grande como sea posible. Este efecto rotacional de una fuerza alrededor del eje z se llama algunas veces torque, pero con mayor frecuencia se le llama momento de una fuerza o, simplemente, momento ![]() . Nótese que el eje z es perpendicular al plano que contiene tanto a
. Nótese que el eje z es perpendicular al plano que contiene tanto a ![]() como a
como a ![]() , además el eje z intersecta al plano en el punto 0.
, además el eje z intersecta al plano en el punto 0.
En general, la fuerza ![]() y el punto O se localizan en el espacio pero la línea de acción de
y el punto O se localizan en el espacio pero la línea de acción de ![]() y el punto O están contenidos en el mismo plano (sombreado) como se indica en la Figura anterior. El momento de
y el punto O están contenidos en el mismo plano (sombreado) como se indica en la Figura anterior. El momento de ![]() con respecto a un eje que pasa por 0 se define como una cantidad vectorial
con respecto a un eje que pasa por 0 se define como una cantidad vectorial ![]() en donde:
en donde:
Magnitud. La magnitud de ![]() es
es ![]()
Dirección. La dirección de ![]() se puede determinar usando la regla de la mano derecha. El procedimiento es el siguiente.
se puede determinar usando la regla de la mano derecha. El procedimiento es el siguiente.
-
Con los cuatro dedos de la mano apuntamos en la dirección del vector posición
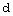 partiendo desde el punto sobre el cual queremos calcular el momento. En la imagen es el punto O:
partiendo desde el punto sobre el cual queremos calcular el momento. En la imagen es el punto O:
Caso 1 La fuerza causa un giro en sentido |
Caso 2 La fuerza causa un giro en sentido |
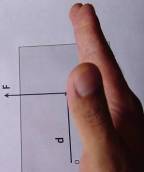 |
 |
-
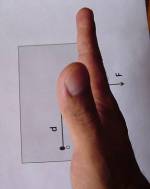
Doblemos los dedos en el sentido de la fuerza. Nota: si no se pueden doblar los dedos en esa dirección tenemos que rotar la mano de manera que sÍ sea posible.
 |
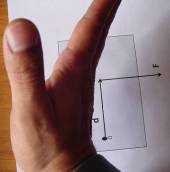
Como se puede apreciar, los dedos no pueden seguir la dirección de F entonces se gira la mano como en las siguientes imágenes |
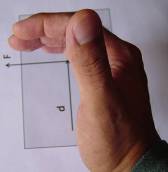 |
1.  |
-
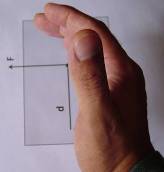
El sentido del giro de nuestros dedos es el que tendrá el momento causado por la fuerza.
 |
 |
-
La dirección del momento, es hacia donde apunta nuestro dedo pulgar, y es perpendicular al plano en donde se encuentran la fuerza y el vector posición.
 |
 |
Este método nos sirve cuando hacemos el análisis escalar de fuerzas, por lo regular en el plano ![]() ; pero cuando realizamos los cálculos en tres dimensiones es mejor realizar el producto de manera vectorial.
; pero cuando realizamos los cálculos en tres dimensiones es mejor realizar el producto de manera vectorial.
Convención de signos:
-
Si el sentido de giro del momento es anti-horario, entonces el momento es positivo y sale del plano sobre el que se encuentran los vectores de posición y fuerza, como se aprecia en la última imagen del lado izquierdo.
-
Si el sentido de giro del momento es en sentido horario, entonces el momento es negativo y entra al plano sobre el que se encuentran los vectores de posición y fuerza, como se aprecia en la última imagen del lado derecho.
V. Forma vectorial
El momento de una fuerza respecto de un eje perpendicular tanto a la fuerza como al vector de posición se define como: ![]()
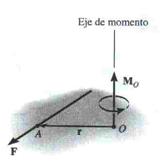
en donde ![]() representa un vector de posición que parte desde O hacia cualquier punto que esté sobre la línea de acción de
representa un vector de posición que parte desde O hacia cualquier punto que esté sobre la línea de acción de ![]() . La magnitud del momento de la fuerza es:
. La magnitud del momento de la fuerza es: ![]() (Véase siguiente figura para relacionar d con r).
(Véase siguiente figura para relacionar d con r).
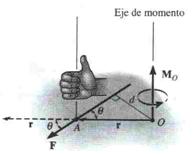
Es posible aplicar la regla de la mano derecha para determinar la dirección del momento de la fuerza, pero para cálculos precisos es necesario desarrollar el producto cruz de la siguiente manera:
El vector![]() podemos expresarlo como:
podemos expresarlo como:
El vector ![]() podemos expresarlo como:
podemos expresarlo como:
Para calcular el producto cruz entre la fuerza y el vector de posición hay que desarrollar el siguiente determinante:
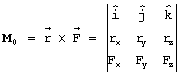
VI. Ejemplo resuelto
Para reforzar los conocimientos adquiridos en esta unidad te presentamos el siguiente ejemplo:

 2
2 3.
3.