Con este objeto de aprendizaje el alumno relacionará los conceptos de momento, aceleración e impulso angular con los correspondientes del movimiento lineal.
Rotación
Momento, aceleración e impulso angular
I. Momento y aceleración angular
Recordando que en el movimiento rectilíneo la fuerza es la que puede causar movimiento o no, dependiendo de las restricciones del cuerpo en cuestión, mientras que en el movimiento rotacional el causante del movimiento es el momento o par que se aplica para que el cuerpo gire, entonces la ecuación análoga a la segunda ley de Newton para el movimiento rotacional es:
|
II. Impulso y momento angular
El impulso y momento lineal se definió en la unidad 5 como :
Sin embargo, al aplicar el principio de impulso y cantidad de movimiento a cuerpos rígidos, lo que interesa son las velocidades de sus centros de masa y sus velocidades angulares. Para lo anterior no basta el principio del impulso y la cantidad de movimiento lineal. Es debido a esto que se necesita definir el principio del impulso y el momento angular para un cuerpo rígido en movimiento plano.
El cuerpo está girando con respecto a un centro de giro “O” como se aprecia en la figura:
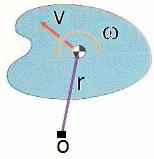
Imagen del libro de Bedford Fowler Dinámica mecánica para ingeniería, Addison Wesley.
Se puede calcular la suma de momentos con respecto a “O” debido a fuerzas y pares externos, y a la razón de cambio del momento angular del cuerpo rígido en la forma:
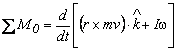
Donde:
es la suma de momentos con respecto al centro de giro “O”
“I” es el momento de inercia de masa del cuerpo rígido respecto a su centro de masa.
es el momento angular debido a la velocidad del centro de masa
Donde:
“r” es la distancia desde el centro de giro “O” hasta el centro de masa del cuerpo
“m” es la masa del cuerpo
“v” es la velocidad lineal del centro de masa
es el vector unitario del eje alrededor del cual de está girando.
es el momento angular debido a la velocidad angular 
y su momento de inercia de masa I también se denota como:
momento angular
Donde H0 se refiere a la cantidad de movimiento angular.
La ecuación anterior expresa el momento angular como la suma de los momentos angulares respecto a “O”: debido a la velocidad del centro de masa, el término es 
y al momento angular respecto al centro de masa, el término es 
. El vector unitario 
es perpendicular al plano de movimiento, y su dirección es definida por la elección de la dirección positiva para el momento y la velocidad angular positiva en dirección anti-horaria.
Si obtenemos el principio del impulso angular y del momento angular, en función del momento total respecto al centro de masa, se tiene:
ésta se puede escribir como:
o también:
si M es constante
Ecuación del impulso y momento lineal cuando se realiza el cálculo con respecto al centro de masa del cuerpo rígido en donde :
es el impulso angular
es el momento angular
es la diferencia del momento angular inicial y el final.
Notemos que esta ecuación no incluye el término 
ya que se está considerando el impulso angular y el momento angular con respecto al centro de giro.
El momento angular promedio con respecto a ”O” en el lapso de tiempo de 
es:
Y la podemos escribir como:
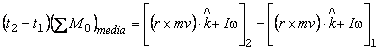
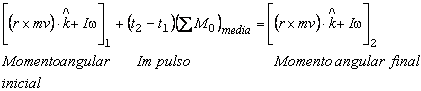
Como podemos apreciar en esta ecuación, si tenemos un momento angular inicial y le damos un impulso mediante un instante de tiempo, obtenemos como resultado un momento angular final.
III. Conservación del momento angular
En unidades anteriores analizamos el caso en el cual las fuerzas externas al sistema de estudio se podían despreciar en comparación con el impacto que es el caso de estudio. Pero ahora vamos a considerar el impacto entre cuerpos rígidos. Cuando éstos chocan entre sí, no sólo se presentan fuerzas, sino que también están presentes momentos que pueden hacer que giren los cuerpos involucrados.
Vamos a analizar el caso en que dos cuerpos A y B chocan como se ve en la siguiente figura.
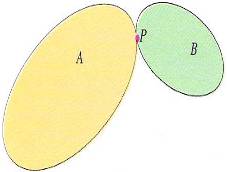
Si en el sistema mostrado las fuerzas externas y pares aplicados a los cuerpos son insignificantes en comparación con los de impacto que A y B ejercen entre sí, su momento angular total respecto a cualquier punto fijo 0 es el mismo antes y después del impacto. Si además A y B ejercen sólo fuerzas entre sí en su punto de impacto P, es decir, ningún par, el momento angular respecto a P de cada cuerpo es el mismo antes y después del impacto.
Es decir, se conserva el momento angular de A respecto a P y el momento angular de B respecto a P.
Escribamos ahora las ecuaciones de impulso y momento angular
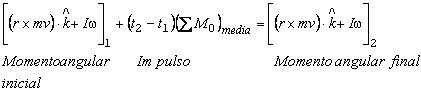
Si no hay fuerzas ni pares (momentos) externas, o son insignificantes en comparación con el impacto el impulso, es cero :
Entonces la ecuación para la conservación del momento angular queda:
Y el coeficiente de restitución es:
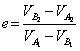
IV. Animación
Observa la siguiente animación y verifica los conceptos estudiados en este apartado.