Con este objeto de aprendizaje se pretende contextualizar al educando en el tema de movimiento armónico
Movimiento periódico
Movimiento armónico
Introducción Muchos tipos de movimiento se repiten una y otra vez, como el péndulo de un reloj con pedestal, las vibraciones sonoras de algún instrumento musical, el movimiento de los pistones de un automóvil, etc. A éstos se les conoce como movimientos periódicos. Una de las características principales de este tipo de movimiento es que tiene una posición de equilibro estable. Cuando se aleja de dicha posición y se suelta, entra en acción una fuerza o momento de torsión que trata de regresarlo a la posición de equilibrio estable. Sin embargo, cuando llega a esta posición, la energía cinética que adquiere no le permite detenerse ahí, sino que lo lleva hasta el otro extremo, desde donde será impulsado nuevamente por la acción de la fuerza o momento de torsión. En condiciones ideales, este proceso podría repetirse eternamente. El ejemplo más sencillo que puedes imaginar es un péndulo en oscilación. Observa las figuras, relaciona cada una de ellas con lo que acabas de leer y, si es necesario, léelo nuevamente. |
I. Movimiento armónico simple. Sistema masa resorte
Para que puedas entender los primeros términos de este tipo de movimiento ocuparemos un sistema masa resorte.
El valor de 0 corresponde a la posición inicial (origen), que es precisamente el momento en el cual el resorte no está estirado ni comprimido. Cuando la masa se jala hacia la derecha (como se aprecia en la anterior figura) hasta un punto A y se suelta, de acuerdo con la ley de Hook, la fuerza de restitución (Fx) genera una oscilación desde A hasta -A. La distancia que existe desde el origen hasta A es conocida como amplitud.
Supongamos que no hay fricción en el sistema mostrado. Realicemos el diagrama de cuerpo libre (DCL) para obtener la ecuación del movimiento del bloque:
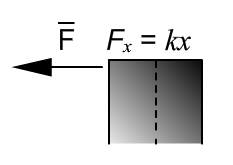
De lo anterior podemos observar que la sumatoria de fuerzas en "y" es cero y que no hay otra fuerza además de la del resorte.
Realicemos la suma de fuerzas para encontrar la ecuación del movimiento del sistema masa resorte:
De acuerdo con la Segunda Ley de Newton:
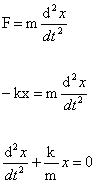
Esta última es la ecuación buscada del movimiento de cualquier sistema masa resorte que no contemple ninguna otra fuerza externa. También se le conoce como la ecuación de movimiento del oscilador armónico simple, que se emplea en muchos problemas físicos relativos a la acústica, la óptica, la mecánica, los circuitos eléctricos y hasta la física atómica.
Círculo de referencia
El círculo de referencia se utiliza para comparar el movimiento de un objeto que se mueve en línea recta con la proyección horizontal de un objeto que se mueve en círculo. Dado que es el movimiento de la proyección el que deseamos estudiar, nos referimos aquí a la posición P del objeto que se mueve en círculo como el punto de referencia. El radio del círculo de referencia es igual a la amplitud de la oscilación horizontal. Si la velocidad lineal 
y la velocidad angular 
del punto de referencia son constantes, la proyección Q se moverá de un lado al otro con un Movimiento Armónico Simple (MAS). Al tiempo se le asigna un valor de cero cuando el punto de referencia se encuentra en B en la siguiente figura.
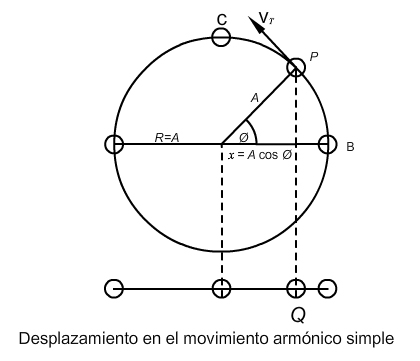
En un momento posterior t el punto de referencia P se habrá movido a través de un ángulo
. El desplazamiento x de la proyección Q es, por lo tanto,
.
Hay que recordar que el ángulo 
, por lo que ahora podemos escribir el desplazamiento como una función de la velocidad angular del punto de referencia.
Aunque la velocidad angular es útil para describir el movimiento del punto de referencia P, no se aplica directamente a la proyección Q. Sin embargo, recordemos que la velocidad angular se relaciona con la frecuencia de revolución mediante:
Con la cual podemos escribir la ecuación:
Donde:
es el desplazamiento angular en radianes.
A es la amplitud del movimiento en las unidades de longitud con las que se esté trabajando (metros o pies).
es la velocidad angular del movimiento sobre el círculo de referencia, también conocida como frecuencia natural circular en rad/seg.
es el tiempo en segundos.
es la frecuencia natural de la oscilación en hertz (Hz).
La ecuación se puede aplicar para calcular el desplazamiento de un cuerpo en movimiento armónico simple de amplitud A y frecuencia f, sin olvidarnos de que el desplazamiento x siempre se mide desde el centro de la oscilación.
En la siguiente animación se pueden observar algunos de los detalles de este tipo de movimiento.
Una solución general de la ecuación diferencial:
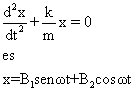
Donde 
son constantes arbitrarias. También se puede expresar como:
Donde:
A es la amplitud del movimiento unidades de longitud que se esté trabajando metros o pies.
determina la posición horizontal de la función cero respecto al origen y se llama ángulo de fase.
es la velocidad angular del movimiento sobre el círculo de referencia también conocida como frecuencia natural circular en rad/seg.
t
es el tiempo en segundos.
En la siguiente gráfica se aprecia la función anterior:
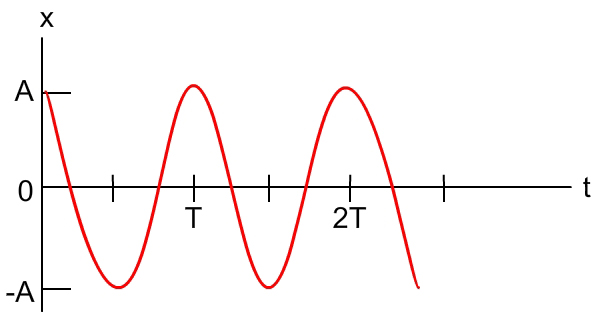
Donde T es el periodo de la oscilación y está definido como:
. La frecuencia natural es 
, y la velocidad angular 
se define para un resorte como:
, donde k es la constante del resorte y m la masa del cuerpo sujeto al resorte.
"No olvides revisar el glosario para que puedas interpretar cada uno de los términos que se emplean en este texto."