Con este objeto de aprendizaje se muestran las características del péndulo y sus similitudes con el movimiento de un resorte.
Movimiento periódico
El péndulo
Introducción Se le llama péndulo simple a un sistema ideal que consta de una masa puntual (del tamaño de un punto, por lo que su masa es despreciable) suspendida de un hilo sin masa y que no se puede estirar. Esta masa oscila de un lado a otro de la posición de equilibrio estable, que en esta ocasión es una línea vertical. La trayectoria de esta masa puntual no es recta, sino que forma un arco cuyo radio es igual a la longitud del hilo "L". A la distancia medida sobre el arco le llamaremos "x"; si el péndulo se mueve con MAS, la fuerza de restitución es directamente proporcional a x o a |
debido a que la fórmula para calcular un arco de circunferencia es 
.
Observa la figura 1:
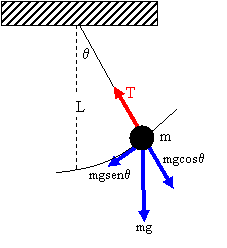
Fig. 1. La fuerza de restitución Fq es la componente tangencial de la fuerza neta
�I. El péndulo
En las secciones anteriores se analizó el movimiento armónico de resortes. En esta sección analizaremos el movimiento de un péndulo oscilando, como el que se aprecia en la imagen:
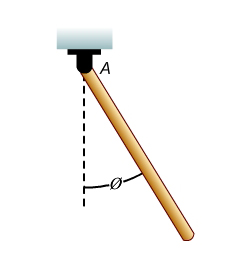
Al analizar este péndulo se llega a la siguiente expresión:
Esta ecuación describe el movimiento del péndulo en cualquier posición de 
. Una simplificación de ésta es cuando hacemos 
para desplazamientos pequeños. Te recomendamos consultar la aplicación Péndulo simple y resorte © 2004 Pearson Educación S.A., y realizar lo siguiente:
-
Espera a que cargue la aplicación.
-
Presiona el botón
. -
Con el puntero del ratón mueve el péndulo a una posición de aproximadamente 1 rad; esta información se ve en el área del gráfico, como se aprecia en la siguiente imagen:
-
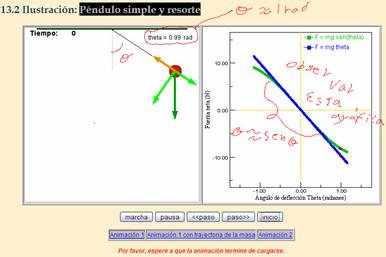
Observa la gráfica que se va a dibujar del lado derecho de la animación, tal como en la figura anterior.
Con lo anterior podemos constatar que realmente 
; entonces la ecuación del movimiento de un péndulo se puede expresar de la siguiente forma para desplazamientos angulares pequeños:
Como se puede observar, las ecuaciones de oscilador resorte-masa y el péndulo produjeron ecuaciones idénticas en forma. Es por esto que se utiliza la misma solución:
Donde 
son constantes arbitrarias; también se puede expresar como:
Donde:
A es la amplitud del movimiento en las unidades de longitud con las que se esté trabajando (metros o pies).
determina la posición horizontal de la función cero respecto al origen y se llama ángulo de fase.
es la velocidad angular del movimiento sobre el círculo de referencia también conocida como frecuencia natural circular en rad/seg.
es el tiempo en segundos.
En la siguiente gráfica se aprecia la función anterior:
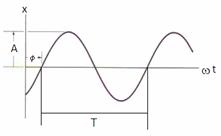
Donde T es el periodo de la oscilación y está definido como:
, y la frecuencia natural es 
.
El periodo también lo podemos calcular como :
para un péndulo simple.
II. Movimiento armónico angular
En la siguiente figura se aprecia un cuerpo sujeto a una barra que está fija en su extremo superior. Si se gira el cuerpo, la barra se comportará como resorte torsional.
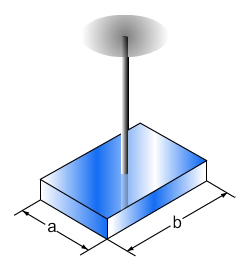
Encontremos su ecuación de movimiento, para hacerlo necesitamos dibujar el Diagrama de Cuerpo Libre
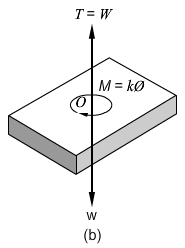
Como la placa se desplaza sólo alrededor del eje de la barra, el momento en el que regresa a su posición original es 
. Este actúa en dirección contraria al desplazamiento angular 
. La aceleración angular 
actúa en la dirección positiva.
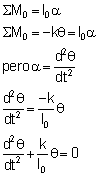
La ecuación a la que se llegó está en la forma estándar del movimiento armónico simple. Lo único que cambia es la frecuencia circular natural, a la que podemos definir como:
Donde:
k es la constante de rigidez torsional o constante de torsión.
es el momento de inercia de masa del cuerpo.