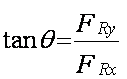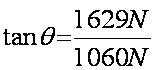Soluci�n del ejemplo 3
Dado que la fuerza resultante corresponde a la suma de los vectores de fuerza de la carga A sobre la carga C que es de repulsión y de la carga B sobre la carga C que es de atracción, el método más conveniente es realizar la descomposición rectangular de las fuerzas y posteriormente realizamos la suma por componentes.
La fuerza de la carga A sobre la carga C es:
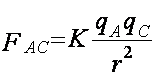
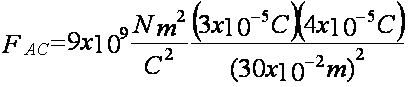
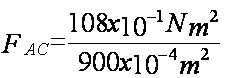
La fuerza es de repulsión puesto que las cargas son del mismo signo y queda dirigida a 60º con respecto a la horizontal, con el origen sobre la carga C, de esta manera, la componente horizontal de la fuerza queda a la derecha:
![]()
Análogamente la componente vertical quedará hacia arriba:
Repitiendo todo el procedimiento para la fuerza de interacción de la carga B sobre la la carga C y considerando que esta es de atracción, obtenemos lo siguiente:
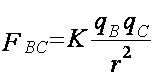
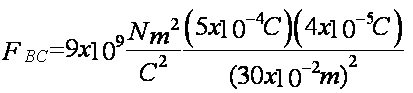
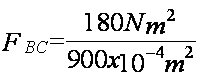
Debido a que las cargas B y C tienen diferente signo, la fuerza es de atracción, con el origen en la carga C la fuerza queda sobre la línea que une a las cargas en la dirección de la carga C a la carga B, es decir 60º abajo de la horizontal, de esta manera la componente horizontal será a la derecha y la componente vertical será hacia abajo.
la componente horizontal de la fuerza entre B y C va hacia la derecha y vale:
la componente vertical de la fuerza entre B y C va hacia abajo y vale:
La componente horizontal de la fuerza resultante, se obtiene sumando las componentes horizontales de las fuerzas aplicadas, de esta manera:
Análogamente la componente vertical de la fuerza resultante, se obtiene sumando las componentes verticales de las fuerzas aplicadas, de esta manera:
Calculamos la resultante usando el teorema de Pitágoras:
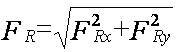
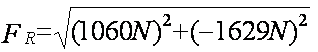
El ángulo lo determinamos usando la función tangente. Para omitir los signos, calcularemos el ángulo medido del semieje positivo de las x’s en el sentido de las manecillas del reloj: